
【题目】如图,∠C=90°,点A、B在∠C的两边上,CA=30,CB=20,连接AB.点P从点B出发,以每秒4个单位长度的速度沿BC的方向运动,到点C停止.当点P与B、C两点不重合时,作PD⊥BC交AB于点D,作DE⊥AC于点E.F为射线CB上一点,使得∠CEF=∠ABC.设点P运动的时间为x秒.
(1)用含有x的代数式表示CE的长.
(2)求点F与点B重合时x的值.
(3)当点F在线段CB上时,设四边形DECP与四边形DEFB重叠部分图形的面积为y(平方单位).求y与x之间的函数关系式.

【答案】①CE=6x;②x=![]() ;③见解析.
;③见解析.
【解析】
(1)首先证明△ABC∽△DBP∽△FEC,即可得出比例式进而得出表示CE的长;
(2)根据当点F与点B重合时,FC=BC,即可得出答案;
(3)首先证明Rt△DOE∽Rt△CEF,得出![]() 即可得出y与x之间的函数关系式.
即可得出y与x之间的函数关系式.
(1)∵∠C=90°,PD⊥BC,
∴DP∥AC,
∴△DBP∽△ABC,四边形PDEC为矩形,
∴![]() ,CE=PD.
,CE=PD.
∴PD=![]() =6x.
=6x.
∴CE=6x;
(2)∵∠CEF=∠ABC,∠C为公共角,
∴△CEF∽△CBA,
∴![]() .
.
∴CF=![]() =9x.
=9x.
当点F与点B重合时,CF=CB,9x=20.
解得x=![]() .
.
(3)当点F与点P重合时,BP+CF=CB,4x+9x=20,
解得x=![]() .
.
当0<x<![]() 时,如图①,
时,如图①,
y=![]() =-51x2+120x.
=-51x2+120x.
当![]() ≤x≤
≤x≤![]() 时,如图②,
时,如图②,
y=![]() DE×DG=
DE×DG=![]() (204x)
(204x)![]() (204x)=
(204x)=![]() (20-4x)2.
(20-4x)2.
(或y=![]() x2
x2![]() x+
x+![]() ).
).


科目:初中数学 来源: 题型:
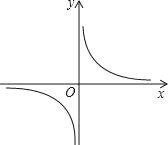
【题目】某气球内充满一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.

(1)写出这一函数的表达式.
(2)当气体体积为1 m3时,气压是多少?
(3)当气球内的气压大于140 kPa时,气球将爆炸,为了安全考虑,气体的体积应不小于多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
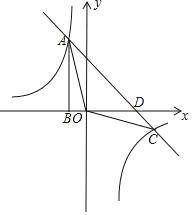
【题目】如图,点A是反比例函数y=![]() 与一次函数y=﹣x﹣k在第二象限内的交点,AB⊥x轴于点B,且S△ABO=3.
与一次函数y=﹣x﹣k在第二象限内的交点,AB⊥x轴于点B,且S△ABO=3.
(1)求这两个函数的表达式;
(2)求一次函数与反比例函数的两个交点A,C的坐标和△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
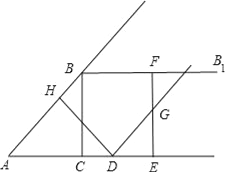
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
(1)当t为何值时,AD=AB,并求出此时DE的长度;
(2)当△DEG与△ACB相似时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
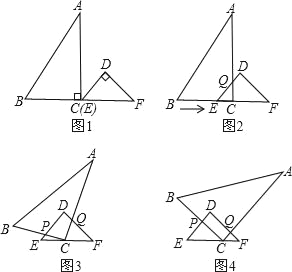
【题目】已知:RT△ABC与RT△DEF中,∠ACB=∠EDF=90°,∠DEF=45°,EF=8cm,AC=16cm,BC=12cm.现将RT△ABC和RT△DEF按图1的方式摆放,使点C与点E重合,点B、C(E)、F在同一条直线上,并按如下方式运动.
运动一:如图2,△ABC从图1的位置出发,以1cm/s的速度沿EF方向向右匀速运动,DE与AC相交于点Q,当点Q与点D重合时暂停运动;
运动二:在运动一的基础上,如图3,RT△ABC绕着点C顺时针旋转,CA与DF交于点Q,CB与DE交于点P,此时点Q在DF上匀速运动,速度为![]() cm/s,当QC⊥DF时暂停旋转;
cm/s,当QC⊥DF时暂停旋转;
运动三:在运动二的基础上,如图4,RT△ABC以1cm/s的速度沿EF向终点F匀速运动,直到点C与点F重合时为止.
设运动时间为t(s),中间的暂停不计时,
解答下列问题
(1)在RT△ABC从运动一到最后运动三结束时,整个过程共耗时 s;
(2)在整个运动过程中,设RT△ABC与RT△DEF的重叠部分的面积为S(cm2),求S与t之间的函数关系式,并直接写出自变量t的取值范围;
(3)在整个运动过程中,是否存在某一时刻,点Q正好在线段AB的中垂线上,若存在,求出此时t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
h | 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t=![]() ;③足球被踢出9.5s时落地:④足球被踢出7.5s时,距离地面的高度是11.25m,其中不正确结论的个数是( )
;③足球被踢出9.5s时落地:④足球被踢出7.5s时,距离地面的高度是11.25m,其中不正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
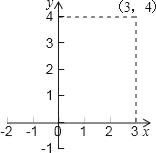
【题目】如图,正方形ABCD是一次函数y=x+1图象的其中一个伴侣正方形.
(1)若某函数是一次函数y=x+1,求它的图象的所有伴侣正方形的边长;
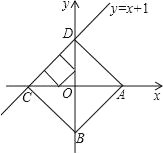
(2)若某函数是反比例函数![]() ,它的图象的伴侣正方形为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数解析式;
,它的图象的伴侣正方形为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数解析式;
(3)若某函数是二次函数y=ax2+c(a≠0),它的图象的伴侣正方形为ABCD,C、D中的一个点坐标为(3,4).写出伴侣正方形在抛物线上的另一个顶点坐标,写出符合题意的其中一条抛物线解析式,并判断你写出的抛物线的伴侣正方形的个数是奇数还是偶数?.(本小题只需直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
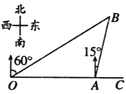
【题目】如图,港口![]() 在观测站
在观测站![]() 的正东方向,
的正东方向,![]() =4km,某船从港口
=4km,某船从港口![]() 出发,沿北偏东
出发,沿北偏东![]() 方向航行一段距离后到达
方向航行一段距离后到达![]() 处,此时从观测站
处,此时从观测站![]() 处侧得该船位于北偏东
处侧得该船位于北偏东![]() 的方向,则该船与观测站之间的距离(即
的方向,则该船与观测站之间的距离(即![]() 的长)为( )
的长)为( )
A. ![]() km B.
km B. ![]() km C.
km C. ![]() km D.
km D. ![]() km
km
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示为一上面无盖的正方体纸盒,现将其剪开展成平面图,如图2所示,已知展开图中每个正方形的边长为1,
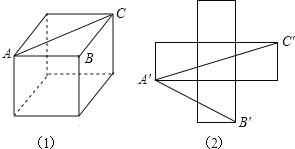
(1)求线段A′C′的长度;
(2)试比较立体图中∠BAC与展开图中∠B′A′C′的大小关系?并写出过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com