
【题目】在△ABC中,AB>BC,直线l垂直平分AC.

(1)如图1,作∠ABC的平分线交直线l于点D,连接AD,CD.
①补全图形;
②判断∠BAD和∠BCD的数量关系,并证明.
(2)如图2,直线l与△ABC的外角∠ABE的平分线交于点D,连接AD,CD.求证:∠BAD=∠BCD.
【答案】(1)①见解析;②∠BAD+∠BCD=180°,证明见解析;(2)见解析.
【解析】
(1)①根据题意画图即可补全图形;
②过点D作DE⊥AB于点E、DF⊥BC交BC的延长线于点F,如图4,根据角平分线的性质和线段垂直平分线的性质可得DE=DF,DA=DC,再根据HL可证Rt△ADE≌Rt△CDF,进而可得∠BAD=∠DCF,进一步即可得出∠BAD和∠BCD的数量关系;
(2)过点D作DH⊥AB于点H,DG⊥CE于点G,如图5,根据角平分线的性质和线段垂直平分线的性质可得DG=DH,DA=DC,再根据HL可证Rt△ADH≌Rt△CDG,进一步即可得出结论.
解:(1)①补全图形如图3;
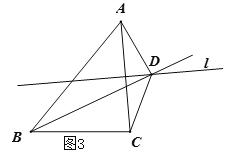
②∠BAD+∠BCD=180°.
证明:过点D作DE⊥AB于点E、DF⊥BC交BC的延长线于点F,如图4,
∵BD平分∠ABC,∴DE=DF,
∵直线l垂直平分AC,∴DA=DC,
∴Rt△ADE≌Rt△CDF(HL),∴∠BAD=∠DCF,
∵∠DCF+∠BCD=180°,
∴∠BAD+∠BCD=180°;

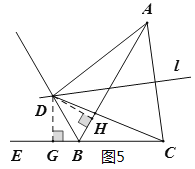
(3)证明:过点D作DH⊥AB于点H,DG⊥CE于点G,如图5,
∵BD平分∠ABE,∴DH=DG,
∵直线l垂直平分AC,∴DA=DC,
∴Rt△ADH≌Rt△CDG(HL),
∴∠BAD=∠BCD,


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx(a≠0)中自变量x和函数值y的部分对应值如下表:
x | … | ﹣2.5 | ﹣2 | ﹣1 | 0 | 0.5 | … |
y | … | ﹣5 | 0 | 4 | 0 | ﹣5 | … |
(1)求二次函数解析式,并写出顶点坐标;
(2)在直角坐标系中画出该抛物线的图象;
(3)若该抛物线上两点A(x1,y1)、B(x2,y2)的横坐标满足x1<x2<﹣1,试比较y1与y2的大小,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线c:y=x2+2x﹣3,将抛物线c平移得到抛物线c′,如果两条抛物线,关于直线x=1对称,那么下列说法正确的是( )
A. 将抛物线c沿x轴向右平移![]() 个单位得到抛物线c′ B. 将抛物线c沿x轴向右平移4个单位得到抛物线c′
个单位得到抛物线c′ B. 将抛物线c沿x轴向右平移4个单位得到抛物线c′
C. 将抛物线c沿x轴向右平移![]() 个单位得到抛物线c′ D. 将抛物线c沿x轴向右平移6个单位得到抛物线c′
个单位得到抛物线c′ D. 将抛物线c沿x轴向右平移6个单位得到抛物线c′
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AOB中,∠AOB=90°,已知点A(﹣1,﹣1),点B在第二象限,OB=![]() ,抛物线
,抛物线![]() 经过点A和B.
经过点A和B.
(1)求点B的坐标;
(2)求抛物线![]() 的对称轴;
的对称轴;
(3)如果该抛物线的对称轴分别和边AO、BO的延长线交于点C、D,设点E在直线AB上,当△BOE和△BCD相似时,直接写出点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在三角形纸片ABC中,∠B=90°,∠A=30°,AC=4,点E在AC上,AE=3.将三角形纸片按图1方式折叠,使点A的对应点![]() 落在AB的延长线上,折痕为ED,
落在AB的延长线上,折痕为ED,![]() 交BC于点F.
交BC于点F.
(1)求∠CFE的度数;
(2)如图2,,继续将纸片沿BF折叠,点![]() 的对应点为
的对应点为![]() ,
,![]() 交DE于点G .求线段DG的长.
交DE于点G .求线段DG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
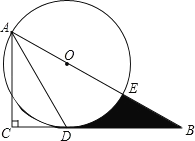
【题目】如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.以AB上某一点O为圆心作⊙O,使⊙O经过点A和点D.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC=3,∠B=30°.
①求⊙O的半径;
②设⊙O与AB边的另一个交点为E,求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解某年级1200名学生每学期参加社会实践活动时间,随机对该年级50名学生进行了调查,结果如下表:
时间(天) | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
人 数 | 1 | 2 | 4 | 5 | 7 | 11 | 8 | 6 | 4 | 2 |
(1)在这个统计中,众数是 ,中位数是 ;
(2)补全下面的频率分布表和频率分布直方图:
分组 | 频数 | 频率 |
3.5~5.5 | 3 | 0.06 |
5.5~7.5 | 9 | 0.18 |
7.5~9.5 | 0.36 | |
9.5~11.5 | 14 | |
11.5~13.5 | 6 | 0.12 |
合 计 | 50 | 1.00 |

(3)请你估算这所学校该年级的学生中,每学期参加社会实践活动时间不少于9天的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 为线段
为线段![]() 上一点,
上一点,![]() ,
, ![]() ,过点
,过点![]() 作直线
作直线![]() ,
,![]() ,在线段
,在线段![]() 上有一点
上有一点![]() ,使得
,使得![]() ,连接
,连接![]() ,若动点
,若动点![]() 从点
从点![]() 开始以每秒
开始以每秒![]() 个单位的速度按
个单位的速度按![]() 的路径运动,当运动到
的路径运动,当运动到![]() 点时停止运动,设出发的时间为
点时停止运动,设出发的时间为![]() 秒.
秒.

(1)当点![]() 在线段
在线段![]() 上运动时,若
上运动时,若![]() ,则
,则![]() 的值为_________;
的值为_________;
(2)求当![]() 为何值时,
为何值时,![]() 为等腰三角形;
为等腰三角形;
(3)若点![]() 为
为![]() 内部射线
内部射线![]() 上一点,当
上一点,当![]() 为等腰直角三角形,求线段
为等腰直角三角形,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米, ![]() ≈1.732)
≈1.732)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com