
【题目】如图,在Rt△AOB中,∠AOB=90°,已知点A(﹣1,﹣1),点B在第二象限,OB=![]() ,抛物线
,抛物线![]() 经过点A和B.
经过点A和B.
(1)求点B的坐标;
(2)求抛物线![]() 的对称轴;
的对称轴;
(3)如果该抛物线的对称轴分别和边AO、BO的延长线交于点C、D,设点E在直线AB上,当△BOE和△BCD相似时,直接写出点E的坐标.

【答案】(1)B(﹣2,2);(2)对称轴是x=1;(3)E的坐标(﹣![]() ,0),(﹣
,0),(﹣![]() ,﹣
,﹣![]() ).
).
【解析】
试题(1)、根据互相垂直的两直线一次项系数的乘积为-1,可得BO的解析式,根据勾股定理可得B点坐标;(2)、根据待定系数法可得函数解析式,根据配方法可得答案;(3)、根据待定系数可得AB的解析式,根据自变量与函数值的对应关系可得E、F点的坐标,分类讨论:△BCD∽△BEO时可得F点坐标;△BCD∽△BOE时根据相似于同一个三角形的两个三角形相似可得△BFO∽△BOE,根据相似三角形的性质可得BF的长,根据勾股定理可得F点坐标.
试题解析:(1)、AO的解析式为y=x,AO⊥BO,则BO的解析式为y=-x,
设B点坐标为(a,-a),由![]() 得:a=2(不符合题意,舍去),或a=-2
得:a=2(不符合题意,舍去),或a=-2
故点B的坐标为(-2,2);
(2)、将A、B点坐标代入函数解析式得: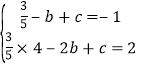 ,解得:
,解得: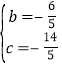 ,
,
∴函数解析式为:![]() ,
,
∴函数的对称轴是:直线x=1;
(3)、点E的坐标为:(﹣![]() ,0),(﹣
,0),(﹣![]() ,﹣
,﹣![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在Δ![]() 中,已知
中,已知![]() 点
点![]() 为
为![]() 中点,点
中点,点![]() 在线段
在线段![]() 上以每秒
上以每秒![]() 的速度由
的速度由![]() 点向
点向![]() 点运动,同时点
点运动,同时点![]() 在线段
在线段![]() 上由
上由![]() 点向
点向![]() 点运动。当点
点运动。当点![]() 的运动速度为每秒____
的运动速度为每秒____![]() 时,能够在某一时刻使得Δ
时,能够在某一时刻使得Δ![]() 与Δ
与Δ![]() 全等
全等

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】瑞士的一位中学教师巴尔末从光谱数据![]() ,…中,成功地发现了其规律,从而得到了巴尔末公式,继而打开了光谱奥妙的大门.请你根据这个规律写出第9个数_____.
,…中,成功地发现了其规律,从而得到了巴尔末公式,继而打开了光谱奥妙的大门.请你根据这个规律写出第9个数_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小方与同学一起去郊游,看到一棵大树斜靠在一小土坡上,他想知道树有多长,于是他借来测角仪和卷尺.如图,他在点C处测得树AB顶端A的仰角为30°,沿着CB方向向大树行进10米到达点D,测得树AB顶端A的仰角为45°,又测得树AB倾斜角∠1=75°.
(1)求AD的长.
(2)求树长AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为3,点E,F分别在射线DC,DA上运动,且DE=DF.连接BF,作EH⊥BF所在直线于点H,连接CH.
(1)如图1,若点E是DC的中点,CH与AB之间的数量关系是 ;
(2)如图2,当点E在DC边上且不是DC的中点时,(1)中的结论是否成立?若成立给出证明;若不成立,说明理由;
(3)如图3,当点E,F分别在射线DC,DA上运动时,连接DH,过点D作直线DH的垂线,交直线BF于点K,连接CK,请直接写出线段CK长的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“已知两线段及一角作三角形”的尺规作图过程.
已知:线段![]() ,
,![]() 及∠O .
及∠O .

求作:△ABC,使得线段![]() ,
,![]() 及∠O分别是它的两边和一角.
及∠O分别是它的两边和一角.
作法:如图,
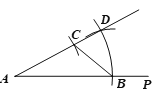
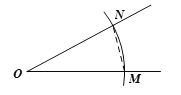
①以点O为圆心,![]() 长为半径画弧,分别交∠O的两边于点M ,N;
长为半径画弧,分别交∠O的两边于点M ,N;
②画一条射线AP,以点A为圆心,![]() 长为半径画弧,交AP于点B;
长为半径画弧,交AP于点B;
③以点B为圆心,MN长为半径画弧,与第②步中所画的弧相交于点D;
④画射线AD;
⑤以点A为圆心,![]() 长为半径画弧,交AD于点C;
长为半径画弧,交AD于点C;
⑥连接BC ,则△ABC即为所求作的三角形.
请回答:
(1)步骤③得到两条线段相等,即 = ;
(2)∠A=∠O的作图依据是 ;
(3)小红说小明的作图不全面,原因是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB>BC,直线l垂直平分AC.

(1)如图1,作∠ABC的平分线交直线l于点D,连接AD,CD.
①补全图形;
②判断∠BAD和∠BCD的数量关系,并证明.
(2)如图2,直线l与△ABC的外角∠ABE的平分线交于点D,连接AD,CD.求证:∠BAD=∠BCD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在半径为6cm的⊙O中,点A是劣弧BC的中点,点D是优弧BC上一点,且∠D=30°,下列四个结论:①OA⊥BC;②BC=6![]() cm;③sin∠AOB=
cm;③sin∠AOB=![]() ;④四边形ABOC是菱形.其中正确结论的序号是( )
;④四边形ABOC是菱形.其中正确结论的序号是( )

A. ①③ B. ①②③④ C. ②③④ D. ①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com