
操作发现
将一副直角三角板如图①摆放,能够发现等腰直角三角板ABC的斜边与含30°角的直角三角板DEF的长直角边DE重合.
问题解决
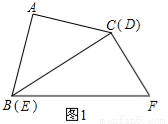
将图①中的等腰直角三角板ABC绕点B顺时针旋转30°,点C落在BF上,AC与BD交于点O,连接CD,如图②.
(1)求证:△CDO是等腰三角形;
(2)若DF=8,求AD的长.

(1)证明见解析;(2)12-4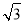 .
.
【解析】
试题分析:(1)根据题意可得BC=DE,进而得到∠BDC=∠BCD,再根据三角形内角和定理计算出度数,然后再根据三角形内角与外角的性质可得∠DOC=∠DBC+∠BCA,进而算出度数,根据角度可得△CDO是等腰三角形;
(2)作AG⊥BC,垂足为点G,DH⊥BF,垂足为点H,首先根据∠F=60°,DF=8,可以算出DH=4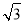 ,HF=4,DB=8
,HF=4,DB=8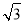 ,BF=16,进而得到BC=8
,BF=16,进而得到BC=8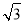 ,再根据等腰三角形的性质可得BG=AG=4
,再根据等腰三角形的性质可得BG=AG=4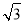 ,证明四边形AGHD为矩形,根据线段的和差关系可得AD长.
,证明四边形AGHD为矩形,根据线段的和差关系可得AD长.
试题解析:(1)证明:由图①知BC=DE,
∴∠BDC=∠BCD,
∵∠DEF=30°,
∴∠BDC=∠BCD=75°,
∵∠ACB=45°,
∵∠DCO+∠BCO=75°
∴∠DCO=30°
∵∠DCO+∠CDO+∠DOC=180°,
∴∠DOC=30°+45°=75°,
∴∠DOC=∠BDC,
∴△CDO是等腰三角形;
(2)【解析】
作AG⊥BC,垂足为点G,DH⊥BF,垂足为点H,
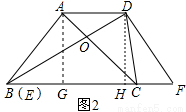
在Rt△DHF中,∠F=60°,DF=8,
∴DH=4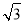 ,HF=4,
,HF=4,
在Rt△BDF中,∠F=60°,DF=8,
∴DB=8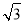 ,BF=16,
,BF=16,
∴BC=BD=8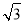 ,
,
∵AG⊥BC,∠ABC=45°,
∴BG=AG=4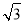 ,
,
∴AG=DH,
∵AG∥DH,AG⊥BC,
∴四边形AGHD为矩形,
∴AD=GH=BF-BG-HF=16-4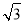 -4=12-4
-4=12-4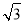 .
.
考点:等腰直角三角形;等腰三角形的判定;含30度角的直角三角形;勾股定理;矩形的判定与性质.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源:2014年北京市密云县中考一模数学试卷(解析版) 题型:解答题
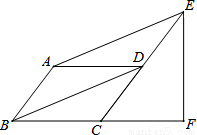
如图,□ABCD中,∠ABC=60°,E,F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF= ,求AB的长.
,求AB的长.
查看答案和解析>>
科目:初中数学 来源:2014届山东省泰安市泰山区初三下学期期末数学试卷(解析版) 题型:填空题
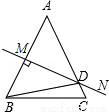
如图,△ABC中,∠A=40°,AB的垂直平分线MN交AC于点D,∠DBC=30°,若AB=m,BC=n,则△DBC的周长为 _________ .
查看答案和解析>>
科目:初中数学 来源:2014届山东省泰安市泰山区初三下学期期末数学试卷(解析版) 题型:填空题
“六•一”期间,小洁的妈妈经营的玩具店进了一纸箱除颜色外都相同的散装塑料球共1000个,小洁将纸箱里面的球搅匀后,从中随机摸出一个球记下其颜色,把它放回纸箱中;搅匀后再随机摸出一个球记下其颜色,把它放回纸箱中;…多次重复上述过程后,发现摸到红球的频率逐渐稳定在0.2,由此可以估计纸箱内红球的个数约是 ________ 个.
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学转化思想(解析版) 题型:填空题
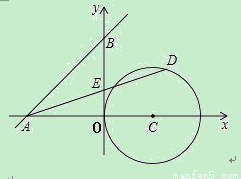
如图,已知直线y=x+4与两坐标轴分别交于A、B两点,⊙C的圆心坐标为 (2,O),半径为2,若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值和最大值分别是 .
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学概率(解析版) 题型:选择题
如图,在平面直角坐标系中,点A1,A2在x轴上,点B1,B2在y轴上,其坐标分别为A1(1,0),A2(2,0),B1(0,1),B2(0,2),分别以A1、A2、B1、B2其中的任意两点与点O为顶点作三角形,所作三角形是等腰三角形的概率是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com