
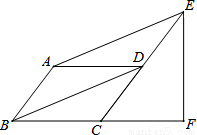
如图,□ABCD中,∠ABC=60°,E,F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF= ,求AB的长.
,求AB的长.
科目:初中数学 来源:2014年北京市房山区中考一模数学试卷(解析版) 题型:解答题
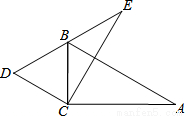
已知:如图,在△DBC中,BC=DC,过点C作CE⊥DC交DB的延长线于点E,过点C作AC⊥BC且AC=EC,连结AB.
求证:AB=ED.
查看答案和解析>>
科目:初中数学 来源:2014年北京市平谷区中考一模数学试卷(解析版) 题型:解答题
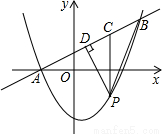
如图,在平面直角坐标系中,直线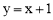 与抛物线y=ax2+bx-3(a≠0)交于A、B两点,点A在x轴上,点B的纵坐标为5.点P是直线AB下方的抛物线上的一动点(不与点A、B重合),过点P作x轴的垂线交直线AB于点C,作PD⊥AB于点D.
与抛物线y=ax2+bx-3(a≠0)交于A、B两点,点A在x轴上,点B的纵坐标为5.点P是直线AB下方的抛物线上的一动点(不与点A、B重合),过点P作x轴的垂线交直线AB于点C,作PD⊥AB于点D.
(1)求抛物线的解析式;
(2)设点P的横坐标为m.
①用含m的代数式表示线段PD的长,并求出线段PD长的最大值;
②连结PB,线段PC把△PDB分成两个三角形,是否存在适合的m的值,使这两个三角形的面积比为1:2.若存在,直接写出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014年北京市平谷区中考一模数学试卷(解析版) 题型:选择题
某校篮球班21名同学的身高如下表:
身高(cm) | 180 | 186 | 188 | 192 | 208 |
人数(个) | 4 | 6 | 5 | 4 | 2 |
则该校篮球班21名同学身高的众数和中位数分别是( )
A.186,188 B.188,186 C.186,186 D.208,188
查看答案和解析>>
科目:初中数学 来源:2014年北京市密云县中考一模数学试卷(解析版) 题型:解答题
如图1所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至CE′F′D′,旋转角为α.
(1)当点D′恰好落在EF边上时,求旋转角α的值;
(2)如图2,G为BC中点,且0°<α<90°,求证:GD′=E′D;
(3)小长方形CEFD绕点C顺时针旋转一周的过程中,△DCD′与△CBD′能否全等?若能,直接写出旋转角α的值;若不能说明理由.

查看答案和解析>>
科目:初中数学 来源:2014年北京市密云县中考一模数学试卷(解析版) 题型:解答题
已知:如图,点A,D,C在同一直线上,AB∥EC,AC=CE,∠B=∠EDC
求证:BC=DE

查看答案和解析>>
科目:初中数学 来源:2014年北京市密云县中考一模数学试卷(解析版) 题型:选择题
如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6, 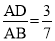 ,则EC的长是( )
,则EC的长是( )
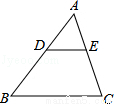
A.4.5 B.8 C.10.5 D.14
查看答案和解析>>
科目:初中数学 来源:2014届山东省泰安市泰山区初三下学期期末数学试卷(解析版) 题型:解答题
操作发现
将一副直角三角板如图①摆放,能够发现等腰直角三角板ABC的斜边与含30°角的直角三角板DEF的长直角边DE重合.
问题解决
将图①中的等腰直角三角板ABC绕点B顺时针旋转30°,点C落在BF上,AC与BD交于点O,连接CD,如图②.
(1)求证:△CDO是等腰三角形;
(2)若DF=8,求AD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com