
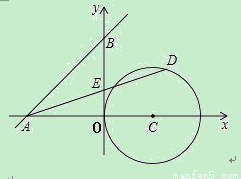
如图,已知直线y=x+4与两坐标轴分别交于A、B两点,⊙C的圆心坐标为 (2,O),半径为2,若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值和最大值分别是 .
8﹣2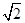 和8+2
和8+2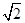
【解析】首先由一次函数解析式求出OA、OB的长,而△ABE中,BE边上的高是OA,且OA为定值,所以求△ABE面积的最小值和最大值,转化为求BE的最小值和最大值。过点A作⊙C的两条切线AD、AD′,当动点运动到D点时,BE最小,即△ABE面积最小;当动点运动到D′点时,BE最大,即△ABE面积最大。最后根据比例求出BE 、BE′的值,进而求出△ABE面积的最小值和最大值.
【解析】
由y=x+4得:
当x=0时,y=4,当y=0时,x=﹣4,
∴OA=4,OB=4,
∵△ABE的边BE上的高是OA,
∴△ABE的边BE上的高是4,
∴要使△ABE的面积最大或最小,只要BE取最大值或最小值即可,
过A作⊙C的两条切线,如图,

当动点运动到D点时,BE最小,即△ABE面积最小;
当动点运动到D′点时,BE最大,即△ABE面积最大;
∵x轴⊥y轴,OC为半径,
∴EE′是⊙C切线,
∵AD′是⊙C切线,
∴OE′=E′D′,
设E′O=E′D′=x,
∵AC=4+2=6,CD′=2,AD′是切线,
∴∠AD′C=90°,由勾股定理得:AD′=4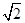 ,
,
∴sin∠CAD′=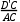 =
= ,
,
∴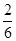 =
= ,
,
解得:x=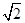 ,
,
∴BE′=4+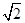 ,BE=4﹣
,BE=4﹣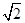 ,
,
∴△ABE的最小值是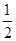 ×(4﹣
×(4﹣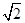 )×4=8﹣2
)×4=8﹣2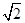 ,
,
最大值是: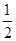 ×(4+
×(4+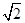 )×4=8+2
)×4=8+2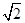 ,
,
故答案为:8﹣2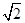 和8+2
和8+2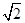 .
.


科目:初中数学 来源:2014届山东省泰安市泰山区初三下学期期末数学试卷(解析版) 题型:解答题
操作发现
将一副直角三角板如图①摆放,能够发现等腰直角三角板ABC的斜边与含30°角的直角三角板DEF的长直角边DE重合.
问题解决
将图①中的等腰直角三角板ABC绕点B顺时针旋转30°,点C落在BF上,AC与BD交于点O,连接CD,如图②.
(1)求证:△CDO是等腰三角形;
(2)若DF=8,求AD的长.

查看答案和解析>>
科目:初中数学 来源:2014届山东省泰安市泰山区初三下学期期末数学试卷(解析版) 题型:选择题
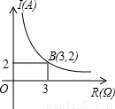
某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例.图表示的是该电路中电流I与电阻R之间函数关系的图象,则用电阻R表示电流I的函数解析式为( )
A.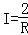 B.
B.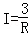 C.
C.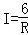 D.
D.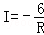
查看答案和解析>>
科目:初中数学 来源:2014届山东省泰安市泰山区初三下学期期末数学试卷(解析版) 题型:选择题
如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线交AB于点D,交AC于点E,连接BE,则∠CBE的度数为( )

A.70° B.80° C.40° D.30°
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学解直角三角形(解析版) 题型:解答题
智能手机如果安装了一款测量软件“Smart Measure”后,就可以测量物高、宽度和面积等.如图,打开软件后将手机摄像头的屏幕准星对准脚部按键,再对准头部按键,即可测量出人体的高度.其数学原理如图②所示,测量者AB与被测量者CD都垂直于地面BC.
(1)若手机显示AC=1m,AD=1.8m,∠CAD=60°,求此时CD的高.(结果保留根号)
(2)对于一般情况,试探索手机设定的测量高度的公式:设AC=a,AD=b,∠CAD= ,即用a、b、
,即用a、b、 来表示CD.(提示:sin2
来表示CD.(提示:sin2 +cos2
+cos2 =1)
=1)

查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学统计(解析版) 题型:填空题
跳远运动员李刚对训练效果进行测试,6次跳远的成绩如下:7.6,7.8,7.7,7.8,8.0,7.9.(单位:m)这六次成绩的平均数为7.8,方差为 .如果李刚再跳两次,成绩分别为7.7,7.9.则李刚这8次跳远成绩的方差 (填“变大”、“不变”或“变小”).
.如果李刚再跳两次,成绩分别为7.7,7.9.则李刚这8次跳远成绩的方差 (填“变大”、“不变”或“变小”).
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学尺规作图(解析版) 题型:解答题
如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点.
(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母(保留作图痕迹,不写作法).
①作∠DAC的平分线AM. ②连接BE并延长交AM于点F.
(2)猜想与证明:试猜想AF与BC有怎样的位置关系和数量关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com