
【题目】如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2 ![]() 则阴影部分图形的面积为( )
则阴影部分图形的面积为( )
A.4π
B.2π
C.π
D.![]()
【答案】D
【解析】解答: 连接OD.
∵CD⊥AB,
∴CE=DE= ![]() CD=
CD= ![]()
故S△OCE=S△ODE ,
即可得阴影部分的面积等于扇形OBD的面积,
又∵∠CDB=30°,
∴∠COB=60°(圆周角定理),
∴OC=2,
故S扇形OBD=60π×22 ![]() ,即阴影部分的面积为
,即阴影部分的面积为 ![]()
故选:D.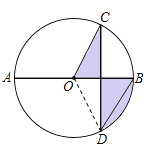
连接OD,则根据垂径定理可得出CE=DE,继而将阴影部分的面积转化为扇形OBD的面积,代入扇形的面积公式求解即可.
【考点精析】掌握垂径定理和圆周角定理是解答本题的根本,需要知道垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.


科目:初中数学 来源: 题型:
【题目】综合题
(1)已知二次函数y=ax2+bx+1的图象经过点(1,3)和(3,﹣5),求a、b的值;
(2)已知二次函数y=﹣x2+bx+c的图象与x轴的两个交点的横坐标分别为1和2.求这个二次函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在AB边上的E处,EQ与BC相交于点F,若AD=8,AE=4,则△EBF周长的大小为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大家看过中央电视台“购物街”节目吗?其中有一个游戏环节是大转轮比赛,转轮上平均分布着5、10、15、20一直到100共20个数字.选手依次转动转轮,每个人最多有两次机会.选手转动的数字之和最大不超过100者为胜出;若超过100则成绩无效,称为“爆掉”.
(1)某选手第一次转到了数字5,再转第二次,则他两次数字之和为100的可能性有多大?
(2)现在某选手第一次转到了数字65,若再转第二次了则有可能“爆掉”,请你分析“爆掉”的可能性有多大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,CN是∠BCE的平分线.
(1)若CM平分∠BCD,求∠MCN的度数;
(2)若CM在∠BCD的内部,且CM⊥CN于C,求证:CM平分∠BCD;
(3)在(2)的条件下,连结BM,BN,且BM⊥BN,∠MBN绕着B点旋转,∠BMC+∠BNC是否发生变化?若不变,求其值;若变化,求其变化范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在杭州西湖风景游船处,如图,在离水面高度为5m的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13m,此人以0.5m/s的速度收绳.10s后船移动到点D的位置,问船向岸边移动了多少m?(假设绳子是直的,结果保留根号)
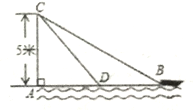
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】适合下列条件的△ABC中,直角三角形的个数为( )
①a=3,b=4,c=5; ②a=6,∠A=45°;③a=2,b=2,c=2![]() ; ④∠A=38°,∠B=52°.
; ④∠A=38°,∠B=52°.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y是x的反比例函数,且当x=-4时,y=![]() ,
,
(1)求这个反比例函数关系式和自变量x的取值范围;
(2)求当x=6时函数y的值.
【答案】(1)![]() (2)
(2)![]()
【解析】整体分析:
(1)由反比例函数的这定义求k值,确定x的取值范围;(2)把x=6代入(1)中求得的反比例函数的解析式.
解:(1)设反比例函数关系式为![]() ,
,
则k=-4×![]() =-2,
=-2,
所以个反比例函数关系式是![]() ,自变量x的取值范围是x≠0.
,自变量x的取值范围是x≠0.
(2)当x=6时, ![]() =
=![]() =-
=-![]() .
.
【题型】解答题
【结束】
18
【题目】如图,函数y=![]() 和y= - x+4的图像交点为A、B,原点为O,求△AOB面积.
和y= - x+4的图像交点为A、B,原点为O,求△AOB面积.
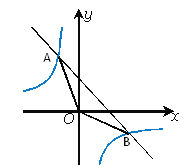
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com