
已知x1,x2是方程x2+2013x+1=0的两个根,则(1+2015x1+x12)(1+2015x2+x22)的值为__________.
4.
【考点】根与系数的关系;一元二次方程的解.
【专题】计算题.
【分析】先根据一元二次方程的解的定义得到x12+2013x1+1=0,x22+2013x2+1=0,则x12+1=﹣2013x1,x22+1=﹣2013x2,于是原式可化简为2x1•2x2,然后利用根与系数的关系计算.
【解答】解:∵x1,x2是方程x2+2013x+1=0的两个根,
∴x12+2013x1+1=0,x22+2013x2+1=0,
∴x12+1=﹣2013x1,x22+1=﹣2013x2,
∴原式=2x1•2x2
=4x1•x2,
∵x1,x2是方程x2+2013x+1=0的两个根,
∴x1•x2=1,
∴原式=4.
故答案为4.
【点评】本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=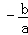 ,x1x2=
,x1x2=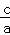 .也考查了一元二次方程的解.
.也考查了一元二次方程的解.


科目:初中数学 来源: 题型:
将点A(3,2)向左平移4个单位长度得到点A′,则点A′关于y轴对称的点的坐标是( )
A.(-3,2)B.(-3,2)C.(1,2)D.(1,-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
把一张圆形纸片和一张含45°角的扇形纸片如图所示的方式分别剪得一个正方形,如果所剪得的 两个正方形边长都是1,那么圆形纸片和扇形纸片的面积比是( )
两个正方形边长都是1,那么圆形纸片和扇形纸片的面积比是( )
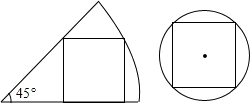
A.4:5 B.2:5 C.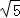 :2 D.
:2 D.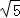 :
:
查看答案和解析>>
科目:初中数学 来源: 题型:
某商场购进一种单价为40元的篮球,如果以单价50元出售,那么每月可售出500个,根据销售经验,售价每提高1元,销售量相应减少10个;
(1)假设销售单价提高x元,那么销售每个篮球所获得的利润是_____ _____元;这种篮球每月的销售量是__________个;(用含x的代数式表示)
_____元;这种篮球每月的销售量是__________个;(用含x的代数式表示)
(2)若商店准备获利8000元,则销售定价为多少元?商店应进货多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
王刚同学在解关于x的方程x2﹣3x+c=0时,误将﹣3x看作+3x,结果解得x1=1,x2=﹣4,则原方程的解为( )
A.x1=﹣1,x2=﹣4 B.x1=1,x2=4 C.x1=﹣1,x2=4 D.x1=2,x2=3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com