练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    抛物线y=a（x+1）（x﹣3）（a≠0）的对称轴是直线(     )

    A．x=1   B．x=﹣1       C．x=﹣3      D．x=3


    A【考点】二次函数的图象．

    【分析】已知抛物线解析式为交点式，通过解析式可求抛物线与x轴的两交点坐标；两交点的横坐标的平均数就是对称轴．

    【解答】解：∵﹣1，3是方程a（x+1）（x﹣3）=0的两根，

    ∴抛物线y=a（x+1）（x﹣3）与x轴交点横坐标是﹣1，3，

    ∵这两个点关于对称轴对称，

    ∴对称轴是x==1．

    故选A．

    【点评】此题考查对称轴的性质：抛物线上的两点纵坐标相同时，对称轴是两点横坐标的平均数．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，小聪把一块含有60°角的直角三角板的两个顶点放在直尺的对边上，并测得∠1=23°，则∠2的度数是（   ）

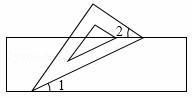
    A．23°       B．22°         C．37°       D．67°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某服装店以每件82元的价格购进了30套保暖内衣，销售时，针对不同的顾客，这30套保暖内衣的售价不完全相同，若以100元为标准，将超过的钱数记为正，不足的钱数记为负，则记录结果如表所示：

    售出件数

    7

    6

    7

    8

    2

     售价（元）

    +5

    +1

     0

    ﹣2

    ﹣5

    请你求出该服装店在售完这30套保暖内衣后，共赚了多少钱？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=1，且经过（﹣1，0）点（如图所示），康康依据图象写出了四个结论：

    ①如果点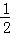（﹣，y1）和（2，y2）都在抛物线上，那么y1＜y2；

    ②b2﹣4ac＞0；

    ③m（am+b）＜a+b（m≠1的实数）；

    ④；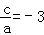

    康康所写结论正确的有__________（只填序号）

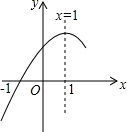
    查看答案和解析>>

    科目：初中数学 来源： 题型：


    微山湖花圃用花盆培育某种花卉，经市场调查发现，出售一盆花的盈利与该盆中花的棵树有关，当每盆栽种3棵时，平均每棵盈利3元，以同样的栽培条件，每盆增加1棵，平均每棵盈利将减少0.5元．设每盆增加种植花卉x棵，每盆盈利y元．

    （1）写出y（元）与x（棵）之间的函数关系式；

    （2）要使每盆盈利达到10元，每盆应当种植该种花卉多少棵？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若关于x的一元二次方程ax2+bx+5=0（a≠0）的解是x=1，则2015﹣a﹣b的值是(     )

    A．2017 B．2018  C．2019 D．2020

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知x1，x2是方程x2+2013x+1=0的两个根，则（1+2015x1+x12）（1+2015x2+x22）的值为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，△ABE≌△ACF．若AB=5，AE=2，BE=4，则CF的长度是(     )

    A．2       B．5       C．4       D．3

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，有一斜坡AB长170m，坡顶离地面的高度BC为80m，求此斜坡的水平距离AC的长度．

    查看答案和解析>>

    同步练习册答案