
抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且经过(﹣1,0)点(如图所示),康康依据图象写出了四个结论:
①如果点(﹣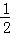 ,y1)和(2,y2)都在抛物线上,那么y1<y2;
,y1)和(2,y2)都在抛物线上,那么y1<y2;
②b2﹣4ac>0;
③m(am+b)<a+b(m≠1的实数);
④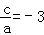 ;
;
康康所写结论正确的有__________(只填序号)
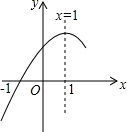
①②③④(只填序号)
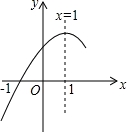
【考点】二次函数图象与系数的关系;二次函数图象上点的坐标特征.
【专题】探究型.
【分析】根据二次函数具有对称性,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,可知x=0和x=2时的函数值一样,由图象可以判断①;根据函数 图象与x轴的交点可判断②;根据函数开口向下,可知y=ax2+bx+c具有最大值,可判断③;根据抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且经过(﹣1,0)点,可知y=0时,x=2,从而可以判断④.
图象与x轴的交点可判断②;根据函数开口向下,可知y=ax2+bx+c具有最大值,可判断③;根据抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且经过(﹣1,0)点,可知y=0时,x=2,从而可以判断④.
【解答】解:∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,
∴x=0与x=2时的函数值相等,由图象可知,x=0的函数值大于x=﹣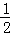 时的函数值.
时的函数值.
∴点(﹣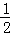 ,y1)和(2,y2)都在抛物线上,则y1<y2(故①正确).
,y1)和(2,y2)都在抛物线上,则y1<y2(故①正确).
∵x=0时,函数图象与x轴两个交点,
∴ax2+bx+c=0时,b2﹣4ac>0(故②正确).
∵由图象可知,x=1时,y=ax2+bx+c取得最大值,
∴当m≠1时,am2+bm+c<a+b+c.
即m(am+b)<a+b(m≠1的实数)(故③正确).
∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且经过(﹣1,0)点,
∴当y=0时,x的值为﹣1或3.
∴ax2+bx+c=0时的两根之积为: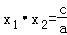 ,x1•x2=(﹣1)×3=﹣3.
,x1•x2=(﹣1)×3=﹣3.
∴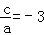 (故④正确).
(故④正确).
故答案为:①②③④.
【点评】本题考查二次函数图象与系数的关系,解题的关键是利用数形结合的思想将二次函数与函数图象结合在一起.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
把一张圆形纸片和一张含45°角的扇形纸片如图所示的方式分别剪得一个正方形,如果所剪得的 两个正方形边长都是1,那么圆形纸片和扇形纸片的面积比是( )
两个正方形边长都是1,那么圆形纸片和扇形纸片的面积比是( )
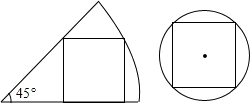
A.4:5 B.2:5 C.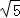 :2 D.
:2 D.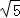 :
:
查看答案和解析>>
科目:初中数学 来源: 题型:
已知,如图,AB是⊙O的直径,C为⊙O上一点,AD垂直于经过点C的直线DE,垂足为点D,AC平分∠DAB.
(1)求证:直线DE是⊙O的切线;
(2)连接BC,猜想:∠ECB与∠CAB的数量关系,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图将4个长、宽分别均为a,b的长方形,摆成了一个大的正方形,利用面积的不同表示方法写 出一个代数恒等式是( )
出一个代数恒等式是( )

A.a2+2ab+b2=(a+b)2 B.a2﹣2ab+b2=(a﹣b)2
C.4ab=(a+b)2﹣(a﹣b)2 D.(a+b)(a﹣b)=a2﹣b2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com