
已知,如图,AB是⊙O的直径,C为⊙O上一点,AD垂直于经过点C的直线DE,垂足为点D,AC平分∠DAB.
(1)求证:直线DE是⊙O的切线;
(2)连接BC,猜想:∠ECB与∠CAB的数量关系,并证明你的猜想.

【考点】切线的判定.
【分析】(1)连接OC,由等腰三角形的性质和已知条件得出∠ACO=∠DAC,证出AD∥OC,再由已知条件得出OC⊥DE,即可得出直线DE是⊙O的切线;
(2)由圆周角定理得出∠ACB=90°,得出∠CAB+∠B=90°,得出∠ECB+∠BCO=90°,由等腰三角形的性质得出∠B=∠BCO,即可得出结论.
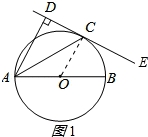
【解答】(1)证明:连接OC,如图1所示:
∵OA=OC,
∴∠BAC=∠ACO,
∵AC平分∠DAB,
∴∠DAC=∠BAC,
∴∠ACO=∠DAC,
∴AD∥OC,
∵AD⊥DE,
∴OC⊥DE,
∴直线DE是⊙O的切线;
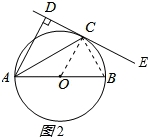
(2)解:如图2所示:∠ECB=∠CAB,理由如下:
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠CAB+∠B=90°,
∵OC⊥DE,
∴∠ECB+∠BCO=90°,
∵OC=OB,
∴∠B=∠BCO,
∴∠ECB=∠CAB.
【点评】本题考查了切线的判定、等腰三角形的性质 、平行线的判定、圆周角定理;熟练掌握切线的判定方法,由等腰三角形的性质得出角相等是解决问题的关键.
、平行线的判定、圆周角定理;熟练掌握切线的判定方法,由等腰三角形的性质得出角相等是解决问题的关键.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
在学习了“25.1.2”概率后,平平和安安两位同学做掷质地均匀的正方体骰子试验,它们共做了120次试验,试验的结果如下表:
| 向上一面的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 出现的次数 | 14 | 18 | 12 | 16 | 40 | 20 |
综合上表,平平说:“如果投掷600次,那么向上一面点数是6的次数正好是100次.”安安说:“一次实验中向上一面点数是5的概率最大”.你认为平平和安安的说法中正确的是( )
A.平平 B.安安 C.都正确 D.都错误
查看答案和解析>>
科目:初中数学 来源: 题型:
抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且经过(﹣1,0)点(如图所示),康康依据图象写出了四个结论:
①如果点(﹣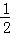 ,y1)和(2,y2)都在抛物线上,那么y1<y2;
,y1)和(2,y2)都在抛物线上,那么y1<y2;
②b2﹣4ac>0;
③m(am+b)<a+b(m≠1的实数);
④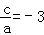 ;
;
康康所写结论正确的有__________(只填序号)
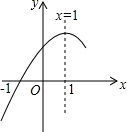
查看答案和解析>>
科目:初中数学 来源: 题型:
若关于x的一元二次方程ax2+bx+5=0(a≠0)的解是x=1,则2015﹣a﹣b的值是( )
A.2017 B.2018 C.2019 D.2020
查看答案和解析>>
科目:初中数学 来源: 题型:
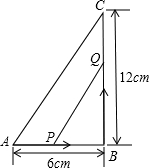
如图,在△ABC中,∠B=90°,点P从点A开始沿AB边向点B以1cm/s的速度移动,Q从点B开始沿BC边向C点以2cm/s的速度移动,如果点P、Q分别从A、B同时出发,几秒钟后,△PBQ的面积等于8cm2?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com