Question

数学活动﹣求重叠部分的面积

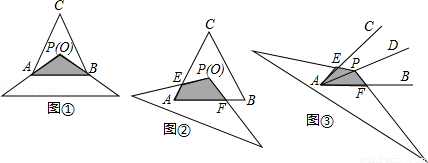
（1）问题情境：如图①，将顶角为120°的等腰三角形纸片（纸片足够大）的顶点P与等边△ABC的内心O重合，已知OA=2，则图中重叠部分△PAB的面积为　 　．

（2）探究1：在（1）的条件下，将纸片绕P点旋转至如图②所示位置，纸片两边分别与AC，AB交于点E，F，图②中重叠部分的面积与图①重叠部分的面积是否相等？如果相等，请给予证明；如果不相等，请说明理由．

（3）探究2：如图③，若∠CAB=α（0°＜α＜90°），AD为∠CAB的角平分线，点P在射线AD上，且AP=2，以P为顶点的等腰三角形纸片（纸片足够大）与∠CAB的两边AC，AB分别交于点E、F，∠EPF=180°﹣α，求重叠部分的面积．（用α或的三角函数值表示）

 

Answer 1

（1）；

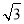（2）图②中重叠部分的面积与图①重叠部分的面积相等，理由见解析；

（3）重叠部分得面积为：4sin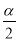cos．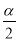

【解析】

试题分析：（1）由点O是等边三角形ABC的内心可以得到∠OAB=∠OBA=30°，结合条件OA=2即可求出重叠部分的面积；

（2）由旋转可得∠FOE=∠BOA，从而得到∠EOA=∠FOB，进而可以证到△EOA≌△FOB，因而重叠部分面积不变；

（3）在射线AB上取一点G，使得PG=PA，过点P作PH⊥AF，垂足为H，方法同（2），可以证到重叠部分的面积等于△PAG的面积，只需求出△PAG的面积就可解决问题．

试题解析：（1）过点O作ON⊥AB，垂足为N，如图①，

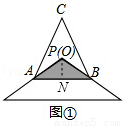
∵△ABC为等边三角形，

∴∠CAB=∠CBA=60°．

∵点O为△ABC的内心

∴∠OAB=∠CAB，∠OBA=∠CBA．

∴∠OAB=∠OBA=30°．

∴OB=OA=2．

∵ON⊥AB，

∴AN=NB，PN=1．

∴AN=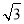

∴AB=2AN=2．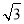

∴S△OAB=AB•PN=．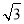

故答案为：；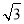

（2）图②中重叠部分的面积与图①重叠部分的面积相等．

连接AO、BO，如图②，

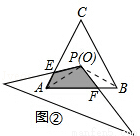
由旋转可得：∠EOF=∠AOB，则∠EOA=∠FOB．

在△EOA和△FOB中，

∴△EOA≌△FOB．

∴S四边形AEOF=S△OAB．

∴图②中重叠部分的面积与图①重叠部分的面积相等；

（3）在射线AB上取一点G，使得PG=PA，过点P作PH⊥AF，垂足为H，如图③，则有AH=GH=AG．

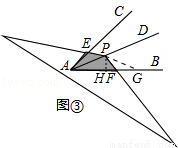
∵∠CAB=α，AD为∠CAB的角平分线，

∴∠PAE=∠PAF=∠CAB=．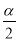

∵PG=PA，

∴∠PGA=∠PAG=．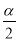

∴∠APG=180°﹣α．

∵∠EPF=180°﹣α，

∴∠EPF=∠APG．

同理可得：S四边形AEPF=S△PAG．

∵AP=2，

∴PH=2sin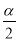，AH=2cos．

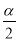∴AG=2AH=4cos．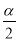

∴S△PAG=AG•PH=4sin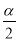cos．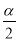

∴重叠部分得面积为：S面积=4sin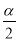cos．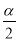

考点：几何变换综合题．