
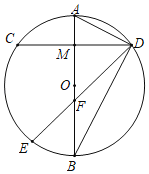
【题目】如图,AB是⊙O的直径,M是OA的中点,弦CD⊥AB于点M,连接AD,点E在BC上,∠CDE=45°,DE交AB于点F,CD=6.
(1)求∠OAD的度数;
(2)求DE的长.
科目:初中数学 来源: 题型:
【题目】如图1,以边长为8的正方形纸片ABCD的边AB为直径作⊙O,交对角线AC于点E.
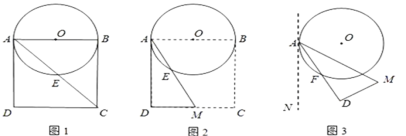
(1)线段AE= ;
(2)如图2,以点A为端点作∠DAM=30°,交CD于点M,沿AM将四边形ABCM剪掉,使Rt△ADM绕点A逆时针旋转(如图3),设旋转角为α(0°<α<150°),旋转过程中AD与⊙O交于点F.
①当α=30°时,请求出线段AF的长;
②当α=60°时,求出线段AF的长;判断此时DM与⊙O的位置关系,并说明理由;
③当α= °时,DM与⊙O相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AC为对角线,延长CD至点E使CE=CA,连接AE.F为AB上的一点,且BF=DE,连接FC.
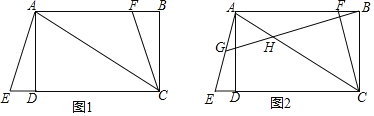
(1)若DE=1,CF=![]() ,求CD的长;
,求CD的长;
(2)如图2,点G为线段AE的中点,连接BG交AC于H,若∠BHC+∠ABG=60°,求证:AF+CE=![]() AC.
AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB是半圆O的直径,正方形OPNM的对角线ON与AB垂直且相等,Q是OP的中点.一只机器甲虫从点A出发匀速爬行,它先沿直径爬到点B,再沿半圆爬回到点A,一台微型记录仪记录了甲虫的爬行过程.设甲虫爬行的时间为t,甲虫与微型记录仪之间的距离为y,表示y与t的函数关系的图象如图2所示,那么微型记录仪可能位于图1中的( )
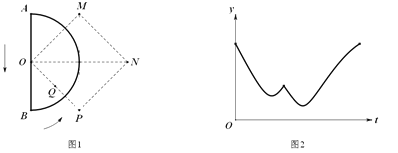
A.点MB.点NC.点PD.点Q
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c交x轴分别于点A(﹣3,0),B(1,0),交y轴正半轴于点D,抛物线顶点为C.下列结论
①2a﹣b=0;
②a+b+c=0;
③当m≠﹣1时,a﹣b>am2+bm;
④当△ABC是等腰直角三角形时,a=![]() ;
;
⑤若D(0,3),则抛物线的对称轴直线x=﹣1上的动点P与B、D两点围成的△PBD周长最小值为3![]() ,其中,正确的个数为( )
,其中,正确的个数为( )
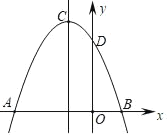
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 已知抛物线![]() 的对称轴是直线x=3,且与x轴相交于A,B两点(B点在A点右侧)与y轴交于C点 .
的对称轴是直线x=3,且与x轴相交于A,B两点(B点在A点右侧)与y轴交于C点 .
(1)求抛物线的解析式和A、B两点的坐标;
(2)若点P是抛物线上B、C两点之间的一个动点(不与B、C重合),则是否存在一点P,使△PBC的面积最大.若存在,请求出△PBC的最大面积;若不存在,试说明理由;
(3)若M是抛物线上任意一点,过点M作y轴的平行线,交直线BC于点N,当MN=3时,求M点的坐标 .
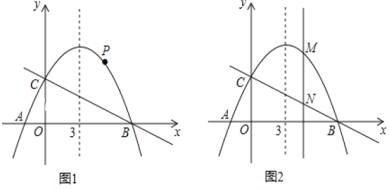
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程 (m-1)x![]() -mx+1=0。
-mx+1=0。
(1)证明:不论m为何值时,方程总有实数根;
(2)若m为整数,当m为何值时,方程有两个不相等的整数根。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】HW公司2018年使用自主研发生产的“QL“系列甲、乙、丙三类芯片共2800万块,生产了2800万部手机,其中乙类芯片的产量是甲类芯片的2倍,丙类芯片的产量比甲,乙两类芯片产量的和还多400万块.这些“QL“芯片解决了该公司2018年生产的全部手机所需芯片的10%.
(1)求2018年甲类芯片的产量.
(2)HW公司计划2020年生产的手机全部使用自主研发的“QL”系列芯片.从2019年起逐年扩大“QL”芯片的产量,2019年、2020年这两年,甲类芯片每年的产量都比前一年增长一个相同的百分数m%,乙类芯片的产量平均每年增长的百分数比m%小1%,丙类芯片的产量每年按相同的数量3200万块递增.这样,2020年的HW公司的手机产量比2018年全年的手机产量多10%,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com