
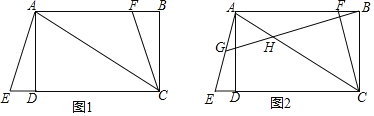
【题目】如图1,在矩形ABCD中,AC为对角线,延长CD至点E使CE=CA,连接AE.F为AB上的一点,且BF=DE,连接FC.
(1)若DE=1,CF=![]() ,求CD的长;
,求CD的长;
(2)如图2,点G为线段AE的中点,连接BG交AC于H,若∠BHC+∠ABG=60°,求证:AF+CE=![]() AC.
AC.
【答案】(1)CD=3;(2)见解析.
【解析】
(1)根据矩形的性质先由勾股定理求得BC的值再通过AC2=AD2+CD2即可求得CD的长;
(2)如图2中,连接CG.作FJ⊥AC于J.通过证明∠BAC=30°,∠ACF=45°即可解决问题.
(1)设CD=x.
∵四边形ABCD是矩形,
∴∠ADC=∠B=90°,AD=BC,
在Rt△BCF中,BC=![]() ,
,
∵AC=CE=x+1,
在Rt△ADC中,∵AC2=AD2+CD2,
∴![]() ,
,
∴x=3,
∴CD=3;
(2)如图2中,连接CG.作FJ⊥AC于J.

∵CA=CE,AG=EG,
∴CG⊥AE,∠ACG=∠ECG,
∵∠AGC=∠ABC=90°,
∴∠AGC+∠ABC=180°,
∴A、G、C、B四点共圆,
∴∠ABG=∠ACG,
∴∠ACG=∠ECG=∠ABG,设∠ACG=∠ECG=∠ABG=x,则∠BAH=∠ACD=2x,∠BHC=∠BAH+∠ABG=3x,
∵∠BHC+∠ABG=60°,
∴4x=60°,
∴x=15°,
∴∠FAJ=30°,∠DAC=∠ACB=60°,∠CAE=75°,
∴∠EAD=15°,
∵DE=BF,∠ADE=∠CBF,AD=BC,
∴![]() ,
,
∴∠BCF=∠DAE=15°,
∴∠FCJ=45°,
∴CJ=FJ,设CJ=FJ=a,则AJ=![]() ,AF=2a,AC=
,AF=2a,AC=![]() ,
,
∴![]() ,
,
∴AF=![]() ,
,
∴AF=![]() ,∵AC=CE,
,∵AC=CE,
∴![]() .
.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
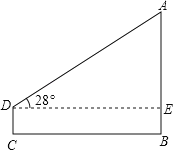
【题目】某数学课外活动小组的同学.利用所学的数学知识,测底部可以到达的学校操场上的旗杆AB高度,他们采用了如下两种方法:
方法1:在地面上选一点C,测得CB为40米,用高为1.6米的测角仪在C处测得旗杆顶部A的仰角为28°;
方法2:在相同时刻测得旗杆AB的影长为17.15米,又测得已有的2米高的竹杆的影长为1.5米.
你认为这两种方法可行吗?若可行,请你任选一种方法算出旗杆高度(精确到0.1米)若不可行,自己另设计一种测量方法(旗杆顶端不能到达),算出旗杆高度(结果可用字母表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
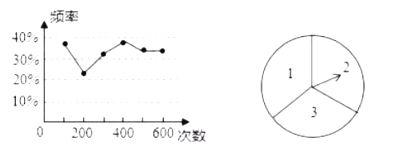
【题目】两名同学在一次用频率估计概率的试验中统计了某一结果出现的频率,绘制出统计图如图所示,则符合这一结果的试验可能是( )
A.抛一枚硬币,正面朝上的概率
B.掷一枚正六面体的骰子,出现![]() 点的概率
点的概率
C.转动如图所示的转盘,转到数字为奇数的概率
D.从装有![]() 个红球和
个红球和![]() 个蓝球的口袋中任取一个球恰好是蓝球的概率
个蓝球的口袋中任取一个球恰好是蓝球的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了提高学生的综合素质,成立了以下社团:![]() .机器人,
.机器人,![]() .围棋,
.围棋,![]() .羽毛球,
.羽毛球,![]() .电影配音.每人只能加入一个社团.为了解学生参加社团的情况,从加社团的学生中随机抽取了部分学生进行调查,并将调查结果绘制成如下两幅不完整的统计图,其中图
.电影配音.每人只能加入一个社团.为了解学生参加社团的情况,从加社团的学生中随机抽取了部分学生进行调查,并将调查结果绘制成如下两幅不完整的统计图,其中图![]() 中
中![]() 所占扇形的圆心角为
所占扇形的圆心角为![]() .
.
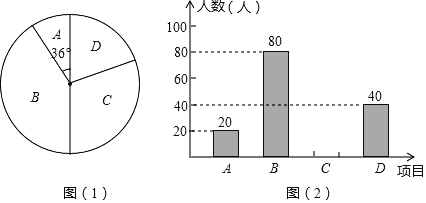
根据以上信息,解答下列问题:
![]() 这次被调查的学生共有 人;
这次被调查的学生共有 人;
![]() 请你将条形统计图补充完整;
请你将条形统计图补充完整;
![]() 若该校共有
若该校共有![]() 学生加入了社团,请你估计这
学生加入了社团,请你估计这![]() 名学生中有多少人参加了羽毛球社团;
名学生中有多少人参加了羽毛球社团;
![]() 在机器人社团活动中,由于甲、乙、丙、丁四人平时的表现优秀,现决定从这四人中任选两名参加机器人大赛.用树状图或列表法求恰好选中甲、乙两位同学的概率.
在机器人社团活动中,由于甲、乙、丙、丁四人平时的表现优秀,现决定从这四人中任选两名参加机器人大赛.用树状图或列表法求恰好选中甲、乙两位同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】临近端午,某超市准备购进某品牌的白粽、豆沙粽、蛋黄粽,三种品种的粽子共1000袋(每袋均为同一品种的粽子),其中白粽每袋12个,豆沙粽每袋8个,蛋黄粽每袋6个.为了推广,超市还计划将三个品种的粽子各取![]() 出来,拆开后重新组合包装,制成A、B两种套装进行特价销售:A套装为每袋白粽4个,豆沙粽4个;B套装为每袋白粽4个,蛋黄粽2个,取出的袋数和套装的袋数均为正整数.若蛋黄粽的进货量不低于总进货量的
出来,拆开后重新组合包装,制成A、B两种套装进行特价销售:A套装为每袋白粽4个,豆沙粽4个;B套装为每袋白粽4个,蛋黄粽2个,取出的袋数和套装的袋数均为正整数.若蛋黄粽的进货量不低于总进货量的![]() ,则豆沙粽最多购进__袋.
,则豆沙粽最多购进__袋.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为节能减排,某公交公司计划购买A型和B型两种环保节能公交车共10辆,若购买A型公交车2辆,B型公交车3辆,共需650万元;若购买A型公交车3辆,B型公交车2辆,共需600万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该线路上A型和B型公交车每辆年均载客量分别为80万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于830万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“三等分角”是数学史上一个著名的问题,但仅用尺规不可能“三等分角”.下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法(如图):将给定的锐角∠AOB置于直角坐标系中,边OB在x轴上、边OA与函数![]() 的图象交于点P,以P为圆心、以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB=
的图象交于点P,以P为圆心、以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB=![]() ∠AOB.要明白帕普斯的方法,请研究以下问题:
∠AOB.要明白帕普斯的方法,请研究以下问题:
(1)设P(![]() ,
,![]() )、R(
)、R(![]() ,
,![]() ),求直线OM对应的函数表达式(用含
),求直线OM对应的函数表达式(用含![]() ,
,![]() 的代数式表示);
的代数式表示);
(2)分别过点P和R作y轴和x轴的平行线,两直线相交于点Q.请说明Q点在直线OM上,并据此证明∠MOB=![]() ∠AOB;
∠AOB;
(3)应用上述方法得到的结论,你如何三等分一个钝角(用文字简要说明)

查看答案和解析>>
科目:初中数学 来源: 题型:
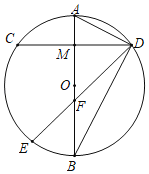
【题目】如图,AB是⊙O的直径,M是OA的中点,弦CD⊥AB于点M,连接AD,点E在BC上,∠CDE=45°,DE交AB于点F,CD=6.
(1)求∠OAD的度数;
(2)求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图(1),在△ABC中,AB=BC=2CD,∠ABC=∠DCB=120°,AC交BD于点E.

(1)如图1:作BM⊥CA于M,求证:△DCE≌△BME;
(2)如图2:点F为BC中点,连接AF交BD于点G,当AB=a时,求线段FG的长度(用含a的代数式表示);
(3)如图3:在(2)的条件下,将△ABG沿AG翻折得到△AKG,延长AK交BD于点H,若BH=5![]() ,求CE的长.
,求CE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com