练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】两名同学在一次用频率估计概率的试验中统计了某一结果出现的频率，绘制出统计图如图所示，则符合这一结果的试验可能是（ ）

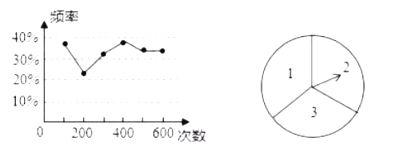
    A.抛一枚硬币，正面朝上的概率

    B.掷一枚正六面体的骰子，出现点的概率

    C.转动如图所示的转盘，转到数字为奇数的概率

    D.从装有个红球和个蓝球的口袋中任取一个球恰好是蓝球的概率

    【答案】D

    【解析】

    根据统计图可知，试验结果在0.33附近波动，即其概率P≈0.33，计算四个选项的概率，约为0.33者即为正确答案．

    解：A、掷一枚硬币，出现正面朝上的概率为，故此选项不符合题意；

    B、掷一枚正六面体的骰子，出现点的概率为，故此选项不符合题意；

    C、转动如图所示的转盘，转到数字为奇数的概率为，故此选项不符合题意；

    D、从装有个红球和个蓝球的口袋中任取一个球恰好是蓝球的概率为，故此选项符合题意．

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，正方形OABC的边OA，OC在坐标轴上，点B的坐标为(－4，4)．点P从点A出发，以每秒1个单位长度的速度沿x轴向点O运动；点Q从点O同时出发，以相同的速度沿x轴的正方向运动，规定点P到达点O时，点Q也停止运动．连接BP，过P点作BP的垂线，与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E，连接PE.设点P运动的时间为t(s)．

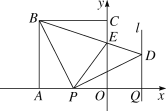
    (1)∠PBD的度数为 ，点D的坐标为 (用t表示)；

    (2)当t为何值时，△PBE为等腰三角形？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】东坡商贸公司购进某种水果成本为20元/，经过市场调研发现，这种水果在未来48天的销售单价（元/）与时间（天）之间的函数关系式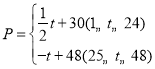，为整数，且其日销售量()与时间（天）的关系如下表：

    时间（天）

    1

    3

    6

    10

    20

    …

    日销售量（）

    118

    114

    108

    100

    80

    …

    （1）已知与之间的变化符合一次函数关系，试求在第30天的日销售量；

    （2）哪一天的销售利润最大？最大日销售利润为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，以边长为8的正方形纸片ABCD的边AB为直径作⊙O，交对角线AC于点E．

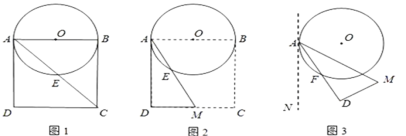
    （1）线段AE=　 ；

    （2）如图2，以点A为端点作∠DAM=30°，交CD于点M，沿AM将四边形ABCM剪掉，使Rt△ADM绕点A逆时针旋转（如图3），设旋转角为α（0°＜α＜150°），旋转过程中AD与⊙O交于点F．

    ①当α=30°时，请求出线段AF的长；

    ②当α=60°时，求出线段AF的长；判断此时DM与⊙O的位置关系，并说明理由；

    ③当α=　 　°时，DM与⊙O相切．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：在平面直角坐标系中，点和点分别在轴和轴的正半轴上，的平分线与正比例函数交于点，且与相交于点，在轴负半轴上有一点.

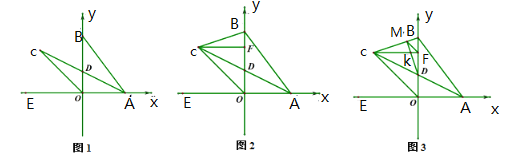
    （1）如图1，求证：；

    （2）如图2，过点作，垂足为，连接，求证：；

    （3）如图3，在（2）的条件下，过点作，垂足为点，交于点，连接，若，，求直线的解析式.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2018年非洲猪瘟疫情暴发后，专家预测，2019年我市猪肉售价将逐月上涨，每千克猪肉的售价y1（元）与月份x（1≤x≤12，且x为整数）之间满足一次函数关系，如下表所示．每千克猪肉的成本y2（元）与月份x（1≤x≤12，且x为整数）之间满足二次函数关系，且3月份每千克猪肉的成本全年最低，为9元，如图所示．

    月份x

    …

    3

    4

    5

    6

    …

    售价y1/元

    …

    12

    14

    16

    18

    …

    （1）求y1与x之间的函数关系式．

    （2）求y2与x之间的函数关系式．

    （3）设销售每千克猪肉所获得的利润为w（元），求w与x之间的函数关系式，哪个月份销售每千克猪肉所第获得的利润最大？最大利润是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了解某市市民上班时常用交通工具的状况，某课题小组随机调查了部分市民（问卷调查表如表所示），并根据调查结果绘制了如图所示的尚不完整的统计图：

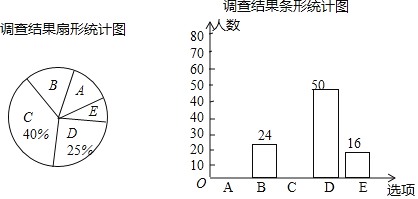
    根据以上统计图，解答下列问题：

    （1）本次接受调查的市民共有　 人；

    （2）扇形统计图中，扇形B的圆心角度数是　 ；

    （3）请补全条形统计图；

    （4）若该市“上班族”约有15万人，请估计乘公交车上班的人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在矩形ABCD中，AC为对角线，延长CD至点E使CE＝CA，连接AE．F为AB上的一点，且BF＝DE，连接FC．

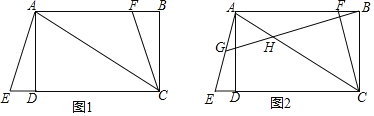
    （1）若DE＝1，CF＝，求CD的长；

    （2）如图2，点G为线段AE的中点，连接BG交AC于H，若∠BHC+∠ABG＝60°，求证：AF+CE＝AC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

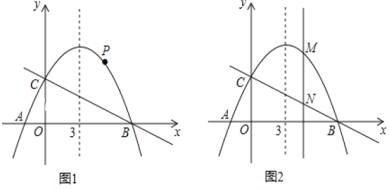
    【题目】如图， 已知抛物线的对称轴是直线x=3，且与x轴相交于A，B两点（B点在A点右侧）与y轴交于C点 ．

    （1）求抛物线的解析式和A、B两点的坐标；

    （2）若点P是抛物线上B、C两点之间的一个动点（不与B、C重合），则是否存在一点P，使△PBC的面积最大．若存在，请求出△PBC的最大面积；若不存在，试说明理由；

    （3）若M是抛物线上任意一点，过点M作y轴的平行线，交直线BC于点N，当MN=3时，求M点的坐标 ．

    查看答案和解析>>

    同步练习册答案