
【题目】如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(-4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).
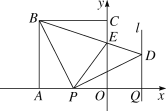
(1)∠PBD的度数为 ,点D的坐标为 (用t表示);
(2)当t为何值时,△PBE为等腰三角形?
【答案】(1)45° (t,t);(2)t=4秒或(4![]() -4)秒
-4)秒
【解析】
(1)易证△BAP≌△PQD,从而得到DQ=AP=t,从而可以求出∠PBD的度数和点D的坐标.
(2)由于∠EBP=45°,故图1是以正方形为背景的一个基本图形,容易得到EP=AP+CE.由于△PBE底边不定,故分三种情况讨论,借助于三角形全等及勾股定理进行求解,然后结合条件进行取舍,最终确定符合要求的t值.
(1)如图1,

由题可得:AP=OQ=1×t=t(秒)
∴AO=PQ.
∵四边形OABC是正方形,
∴AO=AB=BC=OC,
∠BAO=∠AOC=∠OCB=∠ABC=90°.
∵DP⊥BP,
∴∠BPD=90°.
∴∠BPA=90°-∠DPQ=∠PDQ.
∵AO=PQ,AO=AB,
∴AB=PQ.
在△BAP和△PQD中,
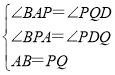
∴△BAP≌△PQD(AAS).
∴AP=QD,BP=PD.
∵∠BPD=90°,BP=PD,
∴∠PBD=∠PDB=45°.
∵AP=t,
∴DQ=t.
∴点D坐标为(t,t).
故答案为:45°,(t,t).
(2)①若PB=PE,则t=0(舍去),
②若EB=EP,
则∠PBE=∠BPE=45°.
∴∠BEP=90°.
∴∠PEO=90°-∠BEC=∠EBC.
在△POE和△ECB中,
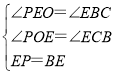
∴△POE≌△ECB(AAS).
∴OE=CB=OC.
∴点E与点C重合(EC=0).
∴点P与点O重合(PO=0).
∵点B(-4,4),
∴AO=CO=4.
此时t=AP=AO=4.
③若BP=BE,
在Rt△BAP和Rt△BCE中,
![]()
∴Rt△BAP≌Rt△BCE(HL).
∴AP=CE.
∵AP=t,
∴CE=t.
∴PO=EO=4-t.
∵∠POE=90°,
∴PE=![]() (4-t).
(4-t).
延长OA到点F,使得AF=CE,连接BF,如图2所示.
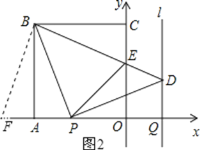
在△FAB和△ECB中,
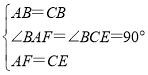
∴△FAB≌△ECB.
∴FB=EB,∠FBA=∠EBC.
∵∠EBP=45°,∠ABC=90°,
∴∠ABP+∠EBC=45°.
∴∠FBP=∠FBA+∠ABP
=∠EBC+∠ABP=45°.
∴∠FBP=∠EBP.
在△FBP和△EBP中,
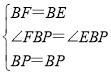
∴△FBP≌△EBP(SAS).
∴FP=EP.
∴EP=FP=FA+AP
=CE+AP.
∴EP=t+t=2t.
∴![]() (4-t)=2t.
(4-t)=2t.
解得:t=4![]() -4
-4
∴当t为4秒或(4![]() -4)秒时,△PBE为等腰三角形.
-4)秒时,△PBE为等腰三角形.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】生产某种农产品的成本每千克20元,调查发现,该产品每天销售量y(千克)与销售单价x(元/千克)满足如下关系:![]() ,设这种农产品的销售利润为w元.
,设这种农产品的销售利润为w元.
(1)求w与x之间的函数关系式.
(2)该产品销售价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)物价部门规定这种产品的销售价不得高于每千克28元,该农户想在这种产品经销季节每天获得150元的利润,销售价应定为每千克多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
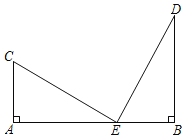
【题目】如图,已知BD⊥AB于点B,AC⊥AB于点A,且BD=3,AC=2,AB=m,在线段AB上找一点E,使△BDE与△ACE相似,若这样的点E有且只有两个,则m的值是______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级(1)班的小华和小红两名学生10次数学测试成绩如下表(表I)所示:
小花 | 70 | 80 | 90 | 80 | 70 | 90 | 80 | 100 | 60 | 80 |
小红 | 90 | 80 | 100 | 60 | 90 | 80 | 90 | 60 | 60 | 90 |
现根据上表数据进行统计得到下表(表Ⅱ):
姓名 | 平均成绩 | 中位数 | 众数 |
小华 | 80 | ||
小红 | 80 | 90 |
(1)填空:根据表I的数据完成表Ⅱ中所缺的数据;
(2)老师计算了小红的方差![]() 请你计算小华的方差并说明哪名学生的成绩较为稳定.
请你计算小华的方差并说明哪名学生的成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船从位于灯塔C的北偏东60°方向,距离灯塔60 n mile的小岛A出发,沿正南方向航行一段时间后,到达位于灯塔C的南偏东45°方向上的B处,这时轮船B与小岛A的距离是( )

A.![]() n mileB.60 n mileC.120 n mileD.
n mileB.60 n mileC.120 n mileD.![]() n mile
n mile
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 已知于x的元二次方程x2﹣6x+2a+5=0有两个不相等的实数根x1,x2.
(1)求a的取值范围;
(2)若x12+x22﹣x1x2≤30,且a为整数,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具商店以每件60元为成本购进一批新型玩具,以每件100元的价格销售则每天可卖出20件,为了扩大销售,增加盈利,尽快减少库存,商店决定采取适当的降价措施,经调查发现:若每件玩具每降价1元,则每天可多卖2件.
(1)若商店打算每天盈利1200元,每件玩具的售价应定为多少元?
(2)若商店为追求效益最大化,每件玩具的售价定为多少元时,商店每天盈利最多?最多盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
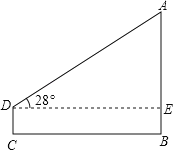
【题目】某数学课外活动小组的同学.利用所学的数学知识,测底部可以到达的学校操场上的旗杆AB高度,他们采用了如下两种方法:
方法1:在地面上选一点C,测得CB为40米,用高为1.6米的测角仪在C处测得旗杆顶部A的仰角为28°;
方法2:在相同时刻测得旗杆AB的影长为17.15米,又测得已有的2米高的竹杆的影长为1.5米.
你认为这两种方法可行吗?若可行,请你任选一种方法算出旗杆高度(精确到0.1米)若不可行,自己另设计一种测量方法(旗杆顶端不能到达),算出旗杆高度(结果可用字母表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两名同学在一次用频率估计概率的试验中统计了某一结果出现的频率,绘制出统计图如图所示,则符合这一结果的试验可能是( )
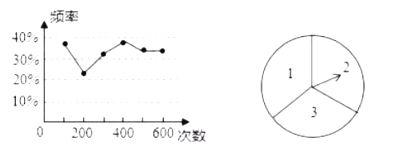
A.抛一枚硬币,正面朝上的概率
B.掷一枚正六面体的骰子,出现![]() 点的概率
点的概率
C.转动如图所示的转盘,转到数字为奇数的概率
D.从装有![]() 个红球和
个红球和![]() 个蓝球的口袋中任取一个球恰好是蓝球的概率
个蓝球的口袋中任取一个球恰好是蓝球的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com