
����Ŀ����ͼ���ھ���ABCD�У�AB=6��BC=8������Q�ӵ�A����������AB������1����λ����/����ٶ������˶���ͬʱ����P�ӵ�B���������ŶԽ���BD����Ҳ��1����λ����/����ٶ������˶������˶�ʱ��Ϊt�루0��t��5������PΪԲ�ģ�PB��Ϊ�뾶�ġ�P��BD��AB����һ������ֱ�ΪE��F������EF��QE�� 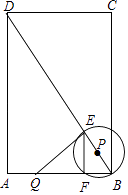
��1����գ�FB=����t�Ĵ���ʽ��ʾ����
��2����tΪ��ֵʱ����Q���F������
��3�����߶�QE���P������������ʱ����t��ȡֵ��Χ��
���𰸡�
��1��![]() t
t
��2���⣺����Q���F����ʱ��AQ+BF=AB��
��t+ ![]() t=6��
t=6��
��t= ![]() s��
s��
�൱t= ![]() sʱ����Q���F����
sʱ����Q���F����
��3���⣺��ֱ��QE���P����ʱ��
�ߡ�BEQ=��A=90�㣬��QBE=��ABD��
���QBE�ס�DBA��
�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��t= ![]() s��
s��
���߶�QE���P�����������㣬
��t��ȡֵ��Χ�� ![]() ��t��
��t�� ![]() ��
��
���������⣺��1����BE�ǡ�P��ֱ�����ı���ABCD�Ǿ��Σ� ���EFB=��A=90��
��Rt��ABC����AD=8��AB=6��
��BD= ![]() =10��
=10��
��EF��AD��
�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��BF= ![]() t��
t��
����Ϊ ![]() t��
t��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���Rt��ABC�У���ABC=90�㣬AB=BC=4����P�ǡ�ABC�ڵ�һ�㣬����PC����PCΪֱ�DZ���PC�����Ϸ�������ֱ��������PCD������AD����AD��BC�����ı���ABCD�����Ϊ12����BP�ij�Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���C=90����ADƽ����BAC��DE��AB��E�������н��ۣ���CD=ED��AC+BE=AB �ۡ�BDE=��BAC ��ADƽ����CDE ��S��ABD��S��ACD=AB��AC��������ȷ���У� ��
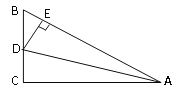
A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��C���߶�AB���е㣬CDƽ�֡�ACE��CEƽ�֡�BCD��CD=CE�� 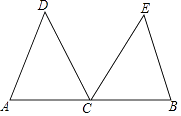
��1����֤����ACD�ա�BCE��
��2������D=53�㣬���B�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����O�ǵȱ���ABC�ڵ���һ�㣬����OA��OB��OC��
��1����ͼ1����֪��AOB=150�㣬��BOC=120�㣬����BOC�Ƶ�C��˳ʱ�뷽����ת60�����ADC��
����DAO�Ķ����� ��
���õ�ʽ��ʾ�߶�OA��OB��OC֮���������ϵ����֤����
��2������AOB=������BOC=�£�
�ٵ�����������ʲô��ϵʱ��OA+OB+OC����Сֵ������ͼ2�л�������������ͼ�Σ���˵�����ɣ�
�����ȱ���ABC�ı߳�Ϊ1��ֱ��д��OA+OB+OC����Сֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A��˫����y= ![]() �ڵ�һ���ķ�֧�ϵ�һ�����㣬����AO���ӳ�����һ��֧�ڵ�B����ABΪ�����ȱߡ�ABC����C�ڵ������ޣ����ŵ�A���˶�����C��λ��Ҳ���ϱ仯������Cʼ����˫����y=
�ڵ�һ���ķ�֧�ϵ�һ�����㣬����AO���ӳ�����һ��֧�ڵ�B����ABΪ�����ȱߡ�ABC����C�ڵ������ޣ����ŵ�A���˶�����C��λ��Ҳ���ϱ仯������Cʼ����˫����y= ![]() ��k��0�����˶�����k��ֵ�� ��
��k��0�����˶�����k��ֵ�� �� 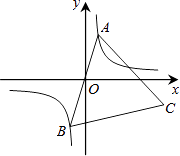
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и��������������Ӧ�Ĵ������ڣ�
�٩�17���ڦУ��۩�|��![]() |����
|����![]() ����
����![]() ���ީ�0.92����
���ީ�0.92����![]() ���ੁ0.
���ੁ0.![]() ����1.2020020002��
����1.2020020002��
��1����ʵ��{�� ��}
��������{�� ��}
������{�� ��}
��2��������9������ѡȡ2����������2�����������á�+�����������¡��е�3�ֲ�ͬ��������Ž�ѡ����4�����������㣨���������ţ���ʹ�ü�����Ϊ���������г�ʽ�Ӳ������� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
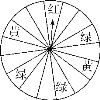
����Ŀ��������ڼ䣬ij�̳�Ϊ�������˿ͣ�������һ����������ת����ת��(ת�̱�ƽ���ֳ�16��)�����涨���˿�ÿ����100Ԫ����Ʒ�����ܻ��һ��תת�̵Ļ��ᣬ���ת��ֹͣ��ָ�����ö���ɫ����ɫ����ɫ���˿;Ϳ��Էֱ�������ܡ�ͯ���顢ˮ�ʱʣ�С�������蹺����125Ԫ����Ʒ������ش��������⣺
(1)С����ý�Ʒ�ĸ����Ƕ��٣�
(2)С���������ܡ�ͯ���顢ˮ�ʱʵĸ��ʷֱ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���г������̼ƻ�Ͷ��7.1��Ԫ����100��A�ͺ�30��B�����г�������B�ͳ�������A�ͳ����۵�6����60Ԫ��
��1����A��B�����ͺŵ����г����۷ֱ��Ƕ���Ԫ��
��2���������ڸþ������ʽ���ţ�Ͷ�빺�����ʽ���5.86��Ԫ��������������������������䣬��ô�����ܹ���B�ͳ���������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com