
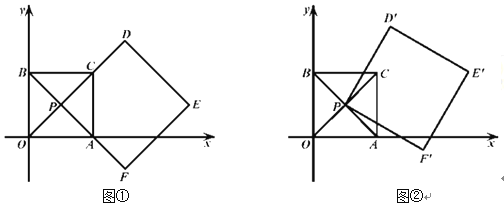
【题目】如图①,在平面直角坐标系中,四边形![]() 是正方形,点
是正方形,点![]() 为正方形
为正方形![]() 对角线的交点,点
对角线的交点,点![]() ,点
,点![]() ,点
,点![]() .分别延长
.分别延长![]() 到
到![]() ,
,![]() 到
到![]() ,使
,使![]() ,
,![]() ,再以
,再以![]() ,
,![]() 为邻边作平行四边形
为邻边作平行四边形![]() .
.
(Ⅰ)求点![]() 的坐标;
的坐标;
(Ⅱ)如图②,将四边形![]() 绕点
绕点![]() 逆时针旋转得四边形
逆时针旋转得四边形![]() ,点
,点![]() ,
,![]() ,
,![]() 旋转后的对应点分别为
旋转后的对应点分别为![]() ,
,![]() ,
,![]() ,旋转角为
,旋转角为![]() .
.
①旋转过程中,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
②在旋转过程中,求![]() 的取值范围(直接写出结果即可).
的取值范围(直接写出结果即可).
【答案】(Ⅰ)![]() ;(Ⅱ)①
;(Ⅱ)①![]() 或
或![]() ,②
,②![]()
【解析】
(Ⅰ)过![]() 作
作![]() 轴于H,根据四边形
轴于H,根据四边形![]() 是正方形和A、B两点的坐标的得出正方形
是正方形和A、B两点的坐标的得出正方形![]() 的边长为2,再根据正方形的性质得出OP=PC=
的边长为2,再根据正方形的性质得出OP=PC=![]() ,结合已知条件利用三角函数得出OH和DH的长即可.
,结合已知条件利用三角函数得出OH和DH的长即可.
(Ⅱ)①当![]() 时,分旋转角
时,分旋转角![]() =
=![]() 和
和![]() 进行讨论,都是过
进行讨论,都是过![]() 作
作![]() 的垂线,垂足记作
的垂线,垂足记作![]() ,利用等腰三角形的性质和三角函数求得
,利用等腰三角形的性质和三角函数求得![]() 的长,从而确定点
的长,从而确定点![]() 的坐标;
的坐标;
②先根据正方形的判定,结合已知条件证出四边形![]() 是正方形,求出对角线PE=4,从而得出点
是正方形,求出对角线PE=4,从而得出点![]() 的运动轨迹是在以B为圆心,4为半径的圆,继而求出
的运动轨迹是在以B为圆心,4为半径的圆,继而求出![]() 的取值范围;
的取值范围;
解:
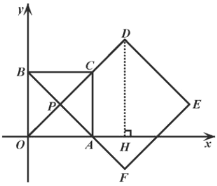
(Ⅰ)过![]() 作
作![]() 轴,垂足记作
轴,垂足记作![]() ,
,
∵四边形![]() 是正方形,
是正方形,![]() ,点
,点![]() ,点
,点![]() .
.
∴正方形![]() 的边长为
的边长为![]() ,
,
∴![]() ,∴
,∴![]()
∵![]() =
=![]() ,∴
,∴![]()
在等腰![]() 中,
中,![]() .
.
∴点![]() 的坐标为
的坐标为![]()
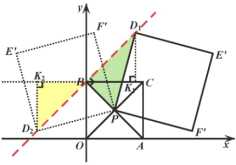
(Ⅱ)①过点![]() 作
作![]() 的垂线
的垂线![]() ,由点
,由点![]() 落在垂线
落在垂线![]() 上.
上.
在![]() 中,
中,
∵![]() ,∴
,∴![]() .
.
∴![]() .
.
∴旋转角![]() 或
或![]()
当![]() 时,
时,
在![]() 中,
中,![]()
过![]() 作
作![]() 的垂线,垂足记作
的垂线,垂足记作![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() .
.
∴点![]() 的坐标为
的坐标为![]()
当![]() 时,
时,
在![]() 中,∵
中,∵![]() ,∴
,∴![]() .
.
∵![]() ,
,![]() ,∴
,∴![]() .
.
在![]() 中,
中,![]() .
.
∴点![]() 的坐标为
的坐标为![]() .
.
综上所述,当![]() 时点
时点![]() 的坐标为
的坐标为![]() 或
或![]()
②∵四边形![]() 平行四边形,AB⊥OC
平行四边形,AB⊥OC
∴平行四边形![]() 是矩形;
是矩形;
∵![]() ,
,![]() ,PC=PA,
,PC=PA,
∴PD=PF,∴矩形![]() 是正方形;
是正方形;
∴PE=4
∴点![]() 在以B为圆心,4为半径的圆上运动;
在以B为圆心,4为半径的圆上运动;
∴![]() ;
;
∴![]() 的取值范围:
的取值范围:![]()


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,在长方形 ABCD 中,AB=5,AD=13,点 E 为 BC 上一点,将△ABE沿 AE 折叠,使点 B 落在长方形内点 F 处,连接 DF 且 DF=12.

(1)试说明:△ADF 是直角三角形;
(2)求 BE 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:①a﹣b+c>0;②3a+b=0;③b2=4a(c﹣n);④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.其中正确结论的是______________(只填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=45°,过OA上到点O的距离分别为1,3,5,7,9,11,的点作OA的垂线与OB相交,得到并标出一组黑色梯形,它们的面积分别为S1,S2,S3,S4,…,观察图中的规律,求出第10个黑色梯形的面积S10=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l1:y=k1x+b过A(0,﹣3),B(5,2),直线l2:y=k2x+2.
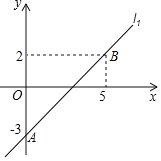
(1)求直线l1的表达式;
(2)当x≥4时,不等式k1x+b>k2x+2恒成立,请写出一个满足题意的k2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的点
中的点![]() 和
和![]() (半径为
(半径为![]() ),给出如下定义:若点
),给出如下定义:若点![]() 关于点
关于点![]() 的对称点为
的对称点为![]() ,且
,且![]() ,则称点
,则称点![]() 为
为![]() 的称心点.
的称心点.
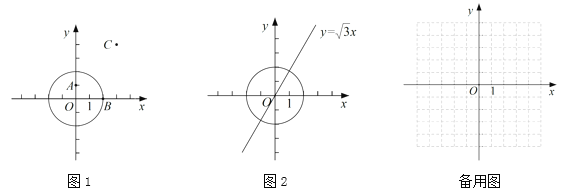
(1)当![]() 的半径为2时,
的半径为2时,
①如图1,在点![]() ,
,![]() ,
,![]() 中,
中,![]() 的称心点是 ;
的称心点是 ;
②如图2,点![]() 在直线
在直线![]() 上,若点
上,若点![]() 是
是![]() 的称心点,求点
的称心点,求点![]() 的横坐标
的横坐标![]() 的取值范围;
的取值范围;
(2)![]() 的圆心为
的圆心为![]() ,半径为2,直线
,半径为2,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,
,![]() .若线段
.若线段![]() 上的所有点都是
上的所有点都是![]() 的称心点,直接写出
的称心点,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,P是边BC上的一动点(不与点B,C重合),点B关于直线AP的对称点为E,连接AE,连接DE并延长交射线AP于点F,连接BF
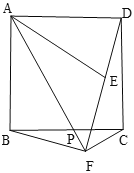
(1)若![]() ,直接写出
,直接写出![]() 的大小(用含
的大小(用含![]() 的式子表示).
的式子表示).
(2)求证:![]() .
.
(3)连接CF,用等式表示线段AF,BF,CF之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】开展阳光体育运动,掌握运动技能,增强身体素质.某校初二年级五月开展了周末一小时兴趣锻炼活动,项目包括:篮球技能、排球技能、足球技能、立定跳远、50米跑,每个同学只选一项参与.王老师为了解学生对各种项目的参与情况,随机调查了部分学生参与哪一类项目(被调查的学生没有不参与的),并将调查结果制成了如下的两个统计图(不完整)请你根据图中所提供的信息,完成下列问题:
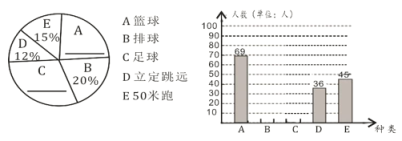
(1)求本次调查的学生人数;
(2)请将两个统计图补充完整,并求出足球项目在扇形统计图中所占圆心角的度数;
(3)若该中学初二年级有![]() 名学生,请估计该校初二学生参与球类项目的人数.
名学生,请估计该校初二学生参与球类项目的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com