
【题目】如图,已知直线y=x+4与两坐标轴分别交于A,B两点,⊙C的圆心坐标为(2,O),半径为2,若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值和最大值分别是 . 
【答案】8﹣2 ![]() 和8+2
和8+2 ![]()
【解析】解:y=x+4,
∵当x=0时,y=4,当y=0时,x=﹣4,
∴OA=4,OB=4,
∵△ABE的边BE上的高是OA,
∴△ABE的边BE上的高是4,
∴要使△ABE的面积最大或最小,只要BE取最大值或最小值即可,
过A作⊙C的两条切线,如图,
当在D点时,BE最小,即△ABE面积最小;
当在D′点时,BE最大,即△ABE面积最大;
∵x轴⊥y轴,OC为半径,
∴EE′是⊙C切线,
∵AD′是⊙C切线,
∴OE′=E′D′,
设E′O=E′D′=x,
∵AC=4+2=6,CD′=2,AD′是切线,
∴∠AD′C=90°,由勾股定理得:AD′=4 ![]() ,
,
∴sin∠CAD′= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得:x= ![]() ,
,
∴BE′=4+ ![]() ,BE=4﹣
,BE=4﹣ ![]() ,
,
∴△ABE的最小值是 ![]() ×(4﹣
×(4﹣ ![]() )×4=8﹣2
)×4=8﹣2 ![]() ,
,
最大值是: ![]() ×(4+
×(4+ ![]() )×4=8+2
)×4=8+2 ![]() ,
,
所以答案是:8﹣2 ![]() 和8+2
和8+2 ![]() .
.


科目:初中数学 来源: 题型:
【题目】定义:两条抛物线顶点都在直线y=x上,且两条抛物线关于原点成中心对称,则称这两条抛物线为一对“友好抛物线”.

(1)抛物线y=2(x-1)2+1如图1所示,请画出它的“友好抛物线”,并直接写出它的解析式;
(确认无误后,请用黑色水笔描黑)
(2)一对“友好抛物线”,其中一条抛物线的解析式为y= -(x+h)2-h,这对“友好抛物线”与y轴交点记为A,B,记AB=n(当A与B重合时,记n=0),现我们来探究n与h的关系;
①当h≥0时,如图2所示,求n与h的函数关系式;
②当h<0时,求n与h的函数关系式;
(3)在(2)的条件下,要使 ![]() ≤n≤
≤n≤ ![]() ,试直接写出h的取值范围.
,试直接写出h的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=kx2+ ![]() x+
x+ ![]() (k是常数).
(k是常数).
(1)若该函数的图象与x轴有两个不同的交点,试求k的取值范围;
(2)若点(1,k)在某反比例函数图象上,要使该反比例函数和二次函数y=kx2+ ![]() x+
x+ ![]() 都是y随x的增大而增大,求k应满足的条件及x的取值范围;
都是y随x的增大而增大,求k应满足的条件及x的取值范围;
(3)若抛物线y=kx2+ ![]() x+
x+ ![]() 与x轴交于A(xA , 0)、B(xB , 0)两点,且xA<xB , xA2+xB2=34,若与y轴不平行的直线y=ax+b经过点P(1,3),且与抛物线交于Q1(x1 , y1)、Q2(x2 , y2)两点,试探究
与x轴交于A(xA , 0)、B(xB , 0)两点,且xA<xB , xA2+xB2=34,若与y轴不平行的直线y=ax+b经过点P(1,3),且与抛物线交于Q1(x1 , y1)、Q2(x2 , y2)两点,试探究 ![]() 是否为定值,并写出探究过程.
是否为定值,并写出探究过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,方格纸中的每个小方格都是边长为1的正方形,Rt△ABC的项点均在格点上.A(﹣6,1)B(﹣3,1)C(﹣3,3) 
(1)将Rt△ABC沿x轴正方向平移5个单位长度后得到Rt△A1B1C1 . 试在图中画出Rt△A1B1C1 , 并写出C1点的坐标;
(2)将Rt△ABC绕点B顺时针旋转90°后得到Rt△A2B2C2 . 试在图中画出Rt△A2B2C2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农庄计划在30亩空地上全部种植蔬菜和水果,菜农小张和果农小李分别承包了种植蔬菜和水果的任务.小张种植每亩蔬菜的工资y(元)与种植面积m(亩)之间的函数如图①所示,小李种植水果所得报酬z(元)与种植面积n(亩)之间函数关系如图②所示. 
(1)如果种植蔬菜20亩,则小张种植每亩蔬菜的工资是元,小张应得的工资总额是元,此时,小李种植水果亩,小李应得的报酬是元;
(2)当10<n≤30时,求z与n之间的函数关系式;
(3)设农庄支付给小张和小李的总费用为w(元),当10<m≤30时,求w与m之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数y= ![]() 和y=﹣
和y=﹣ ![]() 的图象分别是l1和l2 . 设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则△PAB的面积为 .
的图象分别是l1和l2 . 设点P在l1上,PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则△PAB的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市每天能出售甲、乙两种肉集装箱共21箱,且甲集装箱3天的销售量与乙集装箱4天的销售量相同.
(1)求甲、乙两种肉类集装箱每天分别能出售多少箱?
(2)若甲种肉类集装箱的进价为每箱200元,乙种肉类集装箱的进价为每箱180元,现超市打算购买甲、乙两种肉类集装箱共100箱,且手头资金不到18080元,则该超市有几种购买方案?
(3)若甲种肉类集装箱的售价为每箱260元,乙种肉类集装箱的售价为每箱230元,在(2)的情况下,哪种方案获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】神仙居景区门票价格80元/人,景区为吸引游客,对门票价格进行动态管理,非节假日打a折,节假日期间,10人以下(包 括10人)不打折,10人以上超过10人的部分打b折,设游客为x人,门票费用为y元,非节假日门票费用y1(元)及节假日门票费用y2(元)与游客x(人)之间的函数关系如图所示.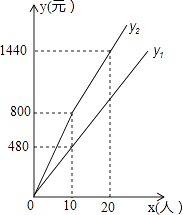
(1)a= , b=;
(2)直接写出y1、y2与x之间的函数关系式;
(3)导游小王6月10日(非节假日)带A旅游团,6月20日(端午节)带B旅游团到神仙居景区旅游,两团共计50人,两次共付门票费用3040元,求A、B两个旅游团各多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com