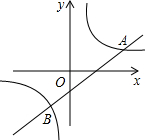
如图所示.一次函数y=kx+b和反比例函数y=$\frac{a}{x}$都经过A两点.则不等式kx+b＞$\frac{a}{x}$的解集为( )A．x＞2B．x＞-1C．-1＜x＜0或x＞2D．x＜-1或0＜x＜2 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

9．

如图所示，一次函数y=kx+b和反比例函数y=$\frac{a}{x}$都经过A（2，1），B（-1，-2）两点，则不等式kx+b＞$\frac{a}{x}$的解集为（　　）

A．

x＞2

B．

x＞-1

C．

-1＜x＜0或x＞2

D．

x＜-1或0＜x＜2

分析根据图形，写出一次函数图象在反比例函数图象上方的x的取值范围即可．

解答解：由图可知，当-1＜x＜0或x＞2时，一次函数图象在反比例函数图象上方，
所以，不等式kx+b＞$\frac{a}{x}$的解集为-1＜x＜0或x＞2．
故选C．

点评本题考查了反比例函数与一次函数的交点问题，仔细观察图形，主要利用了数形结合的思想．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

11．|-M|-|-N|-|-M|+|+2N|-|-3M|（M＞0，N＞0）

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

12．当x=$\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$（a≠0，b²-4ac＞0）时，代数式ax²+bx+c的值是（　　）

A．

B．

$\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$

C．

-$\frac{b}{a}$

D．

$\frac{c}{a}$

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

9．已知5|2a+1|与|4（b-3）|互为相反数，那么ab=-$\frac{3}{2}$．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

4．

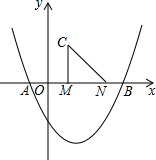如图，二次函数y=$\frac{1}{2}$x²-$\frac{3}{2}$x-2的图象与x轴交于点A，B，点M，N在x轴上，点N在点M右侧，MN=2，以MN为直角边向上作等腰直角三角形CMN，∠CMN=90°，设点M的横坐标为m．
（1）当点C在这条抛物线上时，求m的值．
（2）将线段CN绕点N逆时针旋转90°后，得到对应线段DN．
①当点D在这条抛物线的对称轴上时，求点D的坐标．
②以DN为直角边作等腰直角三角形DNE，当点E在这条抛物线的对称轴上时，求m的值．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

14．若a是实数，则①a²+1，②3|a|+5，③|a|-4，④3a⁴+a³中，一定有平方根的是①②．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

1．下列说法中，正确的有（　　）
①3是9的平方根；
②9的平方根是3；
③-9的平方根是±3；
④平方根等于本身的数是0；
⑤9的算术平方根是3．

A．

2个

B．

3个

C．

4个