
 如图所示,将一副三角板叠放在一起,使直角的顶点重合于点O
如图所示,将一副三角板叠放在一起,使直角的顶点重合于点O分析 (1)根据直角三角板可得∠AOB=∠DOC,再利用等式的性质两边同时减去∠BOD可得∠AOD=∠BOC;
(2)首先把∠AOC化为∠AOB+∠BOC,再根据∠AOB=∠DOC=90°可得∴∠AOC+∠BOD=90°+90°=180°,然后再代入∠AOC=145°,可得∠DOB的度数;
(3)证法与(2)相同.
解答 解:(1)∵∠AOB=∠DOC=90°,
∴∠AOB-∠DOB=∠DOC-∠DOB,
∴∠AOD=∠BOC;
(2)∵∠AOB=∠DOC=90°,
∴∠AOC+∠BOD=∠AOB+∠BOC+∠BOD=∠AOB+∠DOC=90°+90°=180°,
∵∠AOC=145°,
∴∠DOB=180°-145°=35°;
(3)∠AOC+∠DOB=180°,
理由:∵∠AOB=∠DOC=90°,
∴∠AOC+∠BOD,
=∠AOB+∠BOC+∠BOD,
=∠AOB+∠DOC,
=90°+90°=180°.
点评 此题主要考查了余角和补角,关键是理清角之间的关系,掌握如果两个角的和等于90°(直角),就说这两个角互为余角.即其中一个角是另一个角的余角.


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:解答题
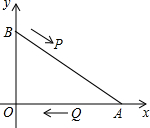 如图,在直角坐标系中,已知点A(8,0)、B(0,6),点P由点B出发沿BA方向向点A作匀速直线运动,速度为每秒3个单位长度,点Q由A出发沿AO(O为坐标原点)方向向点O作匀速直线运动,速度为每秒2个单位长度,连接PQ,若设运动时间为t(0<t<$\frac{10}{3}$)秒.解答如下问题:
如图,在直角坐标系中,已知点A(8,0)、B(0,6),点P由点B出发沿BA方向向点A作匀速直线运动,速度为每秒3个单位长度,点Q由A出发沿AO(O为坐标原点)方向向点O作匀速直线运动,速度为每秒2个单位长度,连接PQ,若设运动时间为t(0<t<$\frac{10}{3}$)秒.解答如下问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 学校要围一个矩形花圃,其一边利用足够长的墙,另三边用篱笆围成,由于园艺需要,还要用一段篱笆将花圃分隔为两个小矩形部分(如图所示),总共36米的篱笆恰好用完(不考虑损耗).设矩形垂直于墙面的一边AB的长为x米(要求AB<AD),矩形花圃ABCD的面积为S平方米.
学校要围一个矩形花圃,其一边利用足够长的墙,另三边用篱笆围成,由于园艺需要,还要用一段篱笆将花圃分隔为两个小矩形部分(如图所示),总共36米的篱笆恰好用完(不考虑损耗).设矩形垂直于墙面的一边AB的长为x米(要求AB<AD),矩形花圃ABCD的面积为S平方米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com