
分析 (1)原式利用算术平方根及立方根定义计算即可得到结果;
(2)原式第一、四项化为最简二次根式,第二项利用负整数指数幂法则计算,第三项利用零指数幂法则计算即可得到结果;
(3)原式各项化为最简二次根式,合并即可得到结果;
(4)原式利用平方根、立方根定义计算即可得到结果.
解答 解:(1)原式=-6+$\frac{3}{2}$+3=-$\frac{3}{2}$;
(2)原式=3$\sqrt{3}$-4+1-2$\sqrt{3}$=$\sqrt{3}$-3;
(3)原式=6$\sqrt{3}$+3$\sqrt{5}$+$\frac{2\sqrt{3}}{3}$-5$\sqrt{5}$=$\frac{20\sqrt{3}}{3}$-2$\sqrt{5}$;
(4)原式=-$\frac{1}{2}$×4+$\frac{1}{2}$+$\frac{1}{2}$=-2+1=-1.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:解答题
 从一副扑克牌中取出的两组牌如图所示,第一组牌是红桃1,2,3,第二组牌是方块1,2,3.将它们分别重新洗匀后,背面朝上放置,再从每组牌中各随机抽取1张.用画树状图(或列表)求抽出的两张牌的牌面数字之和是4的概率.
从一副扑克牌中取出的两组牌如图所示,第一组牌是红桃1,2,3,第二组牌是方块1,2,3.将它们分别重新洗匀后,背面朝上放置,再从每组牌中各随机抽取1张.用画树状图(或列表)求抽出的两张牌的牌面数字之和是4的概率.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
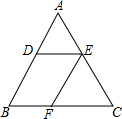 如图:在△ABC中,DE∥BC,EF∥AB,AD=3k,BD=4k,则$\frac{BF}{FC}$的值是( )
如图:在△ABC中,DE∥BC,EF∥AB,AD=3k,BD=4k,则$\frac{BF}{FC}$的值是( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
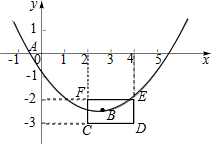 如图,抛物线y=ax2+bx+c与x轴的一个交点A在点(-1,0)和(0,0)之间(包括这两点),顶点B是矩形CDEF上(包括边界和内部)的一个动点,则a的取值范围是$\frac{2}{25}$≤a≤$\frac{3}{4}$.
如图,抛物线y=ax2+bx+c与x轴的一个交点A在点(-1,0)和(0,0)之间(包括这两点),顶点B是矩形CDEF上(包括边界和内部)的一个动点,则a的取值范围是$\frac{2}{25}$≤a≤$\frac{3}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com