练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．（1）计算：20150+（-2）2+6÷（-3）；
    （2）化简：$\frac{{m}^{2}}{m-3}$+$\frac{9}{3-m}$．

    分析 （1）原式第一项利用零指数幂法则计算，第二项利用乘方的意义计算，最后一项利用除法法则计算即可得到结果；
    （2）原式变形后，利用同分母分式的减法法则计算，约分即可得到结果．

    解答 解：（1）原式=1+4+（-2）=5-2=3；
    （2）原式=$\frac{{m}^{2}-9}{m-3}$=$\frac{（m+3）（m-3）}{m-3}$=m+3．

    点评 此题考查了实数的运算，以及分式的加减法，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    20．（1）$-{2^2}-|-7|+3-2×（-\frac{1}{2}）$
    （2）$0.25×{（-2）^3}-[4÷{（-\frac{2}{3}）^2}+1]$
    （3）3x2-1-2x-5+3x-x2
    （4）5a2-[3a-（2a-3）+4a2]．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

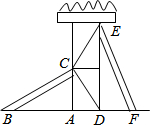    1．某游乐场有两个长度相同的滑梯，要想使左边滑梯BC的高度AC与右边滑梯EF的水平方向的长度DF相等，则两个滑梯的倾斜角∠ABC与∠DFE的大小必须满足什么关系？说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．（1）-$\sqrt{36}$+$\sqrt{2\frac{1}{4}}$-$\root{3}{-27}$
    （2）$\sqrt{27}$-（$\frac{1}{2}$）-2+（1-$\sqrt{3}$）0-$\sqrt{12}$
    （3）$\sqrt{108}$+$\sqrt{45}$+$\sqrt{1\frac{1}{3}}$-$\sqrt{125}$
    （4）（-$\frac{1}{2}$）×（-2）2-$\root{3}{-\frac{1}{8}}$+$\sqrt{（-\frac{1}{2}）^{2}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．单项式-$\frac{{2π{x^2}{y^4}}}{3}$的系数是-$\frac{2}{3}$π，次数是6．多项式$2ab-\frac{1}{3}{a^2}b-1$次数最高的项是-$\frac{1}{3}$a2b，它是三次多项式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．抗震期间，某个别商贩将每件a元的食品提价20%后销售，当地政府及时采取措施，使每件食品的价格在涨价后下降15%，那么降价后每件的价格是（　　）元．
    A．1.2aB．1.02aC．aD．0.18

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．定义一种新运算aφb=a2+b-1，求（-4）φ5的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．如图，要使输出值y大于200，则输入的正整数n最小是41．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．已知：抛物线y1=x2+bx+3与x轴分别交于点A（-3，0），B（m，0）．将y1向右平移4个单位得到y2．
    （1）求b的值；
    （2）求抛物线y2的表达式；
    （3）抛物线y2与y轴交于点D，与x轴交于点E、F（点E在点F的左侧），记抛物线在D、F之间的部分为图象G（包含D、F两点），若直线y=kx+k-1与图象G有一个公共点，请结合函数图象，求直线y=kx+k-1与抛物线y2的对称轴交点的纵坐标t的值或取值范围．

    查看答案和解析>>

    同步练习册答案