
【题目】已知:E是∠AOB的平分线上一点,EC⊥OA ,ED⊥OB ,垂足分别为C、D求证:(1)△OED≌△OEC (2)∠ECD=∠EDC

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】每个小方格是边长为1个单位长度的小正方形,菱形OABC在平面直角坐标系的位置如图所示.
(1)以O为位似中心,在第一象限内将菱形OABC放大为原来的2倍得到菱形OA1B1C1 , 请画出菱形OA1B1C1 , 并直接写出点B1的坐标;
(2)将菱形OABC绕原点O顺时针旋转90°菱形OA2B2C2 , 请画出菱形OA2B2C2 , 并求出点B旋转到点B2的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某体育用品商店,购买50根跳绳和80个毽子共用1120元,购买30根跳绳和50个毽子共用680元.
(1)跳绳、毽子的单价各是多少元?
(2)该店在“元旦”节期间开展促销活动,所有商品按同样的折数打折销售.节日期间购买100根跳绳和100个毽子只需1700元,该店的商品按原价的几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,点
,点![]() 是
是![]() 轴上两点,其中
轴上两点,其中![]() ,点
,点![]() 都在
都在![]() 轴上,
轴上,![]() 在射线
在射线![]() 上(不与点
上(不与点![]() 重合),
重合),![]() ,连结
,连结![]() .
.
(1)求![]() 、
、![]() 的坐标;
的坐标;
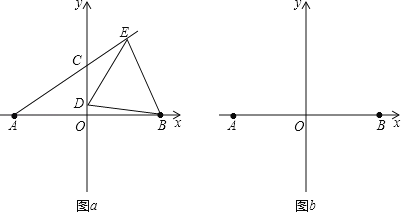
(2)如图![]() ,若
,若![]() 在
在![]() 轴正半轴,
轴正半轴,![]() 在线段
在线段![]() 上,当
上,当![]() 时,求证:
时,求证:![]() 为等边三角形;(提示:连结
为等边三角形;(提示:连结![]() )
)
(3)当![]() 时,在图
时,在图![]() 中画出示意图,设
中画出示意图,设![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:如图1,直线![]() 、
、![]() 、
、![]() 两两相交,交点分别为点A、B、C,点D在线段
两两相交,交点分别为点A、B、C,点D在线段![]() 上,过点D作
上,过点D作![]() 交
交![]() 于点E,过点E作
于点E,过点E作![]() 交
交![]() 于点F.若
于点F.若![]() ,求
,求![]() 的度数.请将下面的解答过程补充完整,并填空
的度数.请将下面的解答过程补充完整,并填空
解:∵![]() ,∴
,∴![]() ________.( )
________.( )
∵![]() ,∴________
,∴________![]() ( )
( )
∴![]() .(等量代换)
.(等量代换)
∵![]() ,∴
,∴![]() ________°.
________°.
应用:如图2,直线![]() 、
、![]() 、
、![]() 两两相交,交点分别为点A、B、C,点D在线段
两两相交,交点分别为点A、B、C,点D在线段![]() 的延长线上,过点D作
的延长线上,过点D作![]() 交
交![]() 于点E,过点E作
于点E,过点E作![]() 交
交![]() 于点F.若
于点F.若![]() ,求
,求![]() 的度数,并仿照(1)进行说明.
的度数,并仿照(1)进行说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,直线AB∥CD,E为AB、CD间的一点,连接EA、EC.

(1)如图①,若∠A=20°,∠C=40°,则∠AEC= °.
(2)如图②,若∠A=x°,∠C=y°,则∠AEC= °.
(3)如图③,若∠A=α,∠C=β,则α,β与∠AEC之间有何等量关系.并简要说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,在面积为3的正方形ABCD中,E,F分别是BC和CD边上的两点,AE⊥BF于点G,且BE=1.
(1)求证:△ABE≌△BCF;
(2)求出△ABE和△BCF重叠部分(即△BEG)的面积;
(3)现将△ABE绕点A逆时针方向旋转到△AB′E′(如图2),使点E落在CD边上的点E′处,问△ABE在旋转前后与△BCF重叠部分的面积是否发生了变化?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,点P是正方形ABCD的BC边上的一点,以DP为边长的正方形DEFP与正方形ABCD在BC的同侧,连接AC,FB.
(1)请你判断FB与AC又怎样的位置关系?并证明你的结论;
(2)若点P在射线CB上运动时,如图②,判断(1)中的结论FB与AC的位置关系是否仍然成立?并说明理由;
(3)当点P在射线CB上运动时,请你指出点E的运动路线,不必说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com