
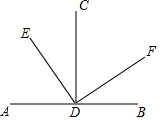
 如图AB⊥CD.垂足为D,ED⊥DF,下列结论正确的有( )
如图AB⊥CD.垂足为D,ED⊥DF,下列结论正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
科目:初中数学 来源: 题型:选择题
| A. | 0是单项式 | B. | 单项式x2y的次数是2 | ||
| C. | 多项式ab+3是一次二项式 | D. | 单项式-$\frac{1}{3}$πx2y的系数是-$\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,中线BE,CD相交于点O,连接DE,则下列判断错误的是( )
如图,在△ABC中,中线BE,CD相交于点O,连接DE,则下列判断错误的是( )| A. | DE是△ABC的中位线 | B. | 点O是△ABC的重心 | ||
| C. | △DEO∽△CBO | D. | $\frac{{S}_{△DOE}}{{S}_{△ADE}}$=$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 每天零花钱(元) | 0 | 5 | 10 | 15 | 20 |
| 人数 | 2 | 3 | 2 | 6 | 2 |
| A. | 众数是20元 | B. | 平均数是11元 | C. | 极差是15元 | D. | 中位数是10元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
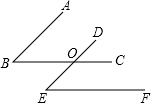 如图,已知AB∥DE,∠B=∠E,求证:BC∥EF.
如图,已知AB∥DE,∠B=∠E,求证:BC∥EF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com