
【题目】如图,在锐角三角形ABC中,∠BAC=60°,BF,CE为高,点D为BC的中点,连接EF,ED,FD,有下列四个结论:①ED=FD;②∠ABC=60°时,EF∥BC;③BF=2AF;④AF:AB=AE:AC.其中正确的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
①由BF、CE为高,D为BC的中点,根据直角三角形斜边上的中线等于斜边的一半,即可证得FD=ED;
②由两角对应相等,易证得△AEF∽△ABC,然后由∠BAC=60°与∠ABC=60°,可得△ABC是等边三角形,则易得∠AEF=∠ABC=60°,即可得EF∥BC;
③根据锐角三角函数的定义,可得③错误;
④可证△ABF∽△ACE,可得结论.
①∵BF、CE为高,
∴∠BEC=∠BFC=90°,
∵D为BC的中点,
∴FD=ED,
故①正确;
②∵BF、CE为高,
∴∠BFA=∠CEA=90°,
∵∠A=∠A,
∴△BFA∽△CEA,
∵∠BAC=60°,∠ABC=60°,
∴△ABC是等边三角形,
∴△AEF也是等边三角形,
∴∠AEF=∠ABC=60°,
∴EF∥BC,
故②正确;
③∵∠ABC=60°,
tan60°=![]() ,
,
∴BF=![]() AF,
AF,
故③错误;
④∵∠AFB=∠AEC=90°,∠A=∠A,
∴△ABF∽△ACE,
得AF:AB=AE:AC.
故④正确;
本题正确的个数有3个:①②④;
故选C.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.阜阳市某家快递公司,2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率?
(2) 如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是数轴的一部分,其单位长度为a,已知△ABC中,AB=3a,BC=4a,AC=5a. ![]()
(1)用直尺和圆规作出△ABC(要求:使点A,C在数轴上,保留作图痕迹,不必写出作法);
(2)记△ABC的外接圆的面积为S圆 , △ABC的面积为S△ , 试说明 ![]() >π.
>π.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细阅读下面例题,然后按要求解答问题:
例题:已知二次三项式 ![]() 有一个因式是
有一个因式是 ![]() ,求另一个因式以及
,求另一个因式以及 ![]() 的值.
的值.
解法一:设另一个因式为 ![]() ,
,
得 ![]() ,
,
则 ![]() ,
,
![]() ,
,
解得 ![]() ,
,
![]() 另一个因式为
另一个因式为 ![]() ,
,![]() 的值为
的值为 ![]() .
.
解法二:∵二次三项式 x2-4x+m 有一个因式是 (x+3),
∴当x+3=0,即x=-3时,x2-4x+m=0.
把x=-3代入x2-4x+m=0,
得m=-21,
而x2-4x-21=(x+3)(x-7).
问题:分别仿照以上两种方法解答下面问题:
(1)已知二次三项式 ![]() 有一个因式是
有一个因式是 ![]() ,求另一个因式以及
,求另一个因式以及 ![]() 的值.
的值.
解法一: 解法二:
(2)直接回答:
已知关于x的多项式 2x3![]() (3
(3![]() k)x2
k)x2![]() 2x
2x![]() 1有一个因式是
1有一个因式是 ![]() 1,则k的值为_________.
1,则k的值为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,∠B=60°,边AB=BC=8cm,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速运动,其中点P运动的速度是每秒1cm,点Q运动的速度是每秒2cm,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t秒.
解答下列问题:
(1)AP= ,BP= ,BQ= .(用含t的代数式表示,t≤4)
(2)当点Q到达点C时,PQ与AB的位置关系如何?请说明理由.
(3)在点P与点Q的运动过程中,△BPQ是否能成为等边三角形?若能,请求出t,若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个长方形运动场被分隔成![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 共
共![]() 个区,
个区, ![]() 区是边长为
区是边长为![]() 的正方形,
的正方形, ![]() 区是边长为
区是边长为![]() 的正方形.
的正方形.
(1)列式表示每个![]() 区长方形场地的周长,并将式子化简;
区长方形场地的周长,并将式子化简;
(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)如果![]() ,
, ![]() ,求整个长方形运动场的面积.
,求整个长方形运动场的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
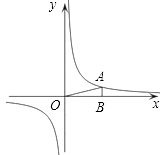
【题目】如图,在直角坐标系中,O为坐标原点.已知反比例函数y= ![]() (k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为
(k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为 ![]() .
.
(1)求k和m的值;
(2)点C(x,y)在反比例函数y= ![]() 的图象上,求当1≤x≤3时函数值y的取值范围;
的图象上,求当1≤x≤3时函数值y的取值范围;
(3)过原点O的直线l与反比例函数y= ![]() 的图象交于P、Q两点,试根据图象直接写出线段PQ长度的最小值.
的图象交于P、Q两点,试根据图象直接写出线段PQ长度的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+3|+(b﹣2)2=0.
(1)求A、B两点的对应的数a、b;
(2)点C在数轴上对应的数为x,且x是方程2x+1=![]() x﹣8的解.
x﹣8的解.
①求线段BC的长;
②在数轴上是否存在点P,使PA+PB=BC?求出点P对应的数;若不存在,说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别延长ABCD的边BA、DC到点E、H,使得AE=AB,CH=CD,连接EH,分别交AD、BC于点F、G. 求证:△AEF≌△CHG.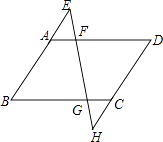
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com