
分析 (1)去括号,然后移项、合并同类项,系数化成1即可求解.
(2)先分别解每个不等式,然后借助数轴确定公共部分即不等式组的解集.
(3)先分别解每个不等式,然后借助数轴确定无公共部分即不等式组无解.
(4)首先解方程组,利用a表示出x,y的值,然后根据x>0,y<0,列不等式组求得a的范围,根据a的范围,以及绝对值的性质即可化简.
解答 解:(1)去括号得:10x-18≤x+12-6x
移项、合并同类项得:15x≤30
系数化为1得:x≤2,
在数轴上表示不等式的解集:
(2)$\left\{\begin{array}{l}{2x+4≤0①}\\{\frac{1}{2}(x+8)-2≥0②}\end{array}\right.$
解不等式①,得x≤-2;
解不等式②,得x≥-4;
因此,原不等式组的解集为-4≤x≤-2,
在数轴上表示不等式的解集: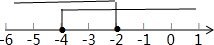
(3)$\left\{\begin{array}{l}{\frac{x-2}{7}≥0①}\\{-2x-3<1-3x②}\end{array}\right.$
由①得,x≥2;
由②得,x<4;
所以不等式的解集为2≤x<4;
在数轴上表示为: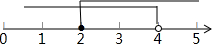
(4)解方程得:$\left\{\begin{array}{l}{x=a+2}\\{y=2a-1}\end{array}\right.$,
∵x>0,y<0,
∴$\left\{\begin{array}{l}{a+2>0}\\{2a-1<0}\end{array}\right.$,
解得:-2<a<$\frac{1}{2}$;
$|{a+2}|-|{a-\frac{1}{2}}|$
=a+2+a-$\frac{1}{2}$
=2a+$\frac{3}{2}$.
点评 本题考查了解一元一次不等式(组),求不等式组的解集,要遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了,利用此规律得出不等式的解集是解题关键.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:解答题
| 听号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 与标准质量的差/g | -10 | +5 | 0 | +5 | 0 | 0 | -5 | 0 | +5 | +10 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 点P在圆外 | B. | 点P在圆内 | ||
| C. | 点P不在圆上 | D. | 点P在圆外或点P在圆内 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ab-4b+3a-12 | B. | ab-4a+3b-12 | C. | ab-4b+3a+12 | D. | ab-4a+3b+12. |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
| 增减 | +6 | -3 | -2 | +10 | -8 | +18 | -10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com