
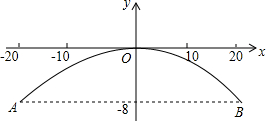
 一抛物线形的石拱桥在如图所示的坐标系中,桥的最大高度为8m,跨度为40m.
一抛物线形的石拱桥在如图所示的坐标系中,桥的最大高度为8m,跨度为40m.分析 (1)根据题意,抛物线的顶点坐标是(0,0),并且过(20,-8),利用抛物线的顶点坐标式待定系数法求它的表达式即可;
(2)把x=5代入函数表达式,解方程即可.
解答 解:(1)设抛物线的解析式为:y=ax2,
∵抛物线过(20,-8),
根据题意代入,得a=-$\frac{1}{50}$,
即得抛物线的解析式为y=-$\frac{1}{50}$x2;
(2)把x=5代入函数表达式,得y=-$\frac{1}{50}$×52=-$\frac{1}{2}$,
∴距y轴5m处的石拱的高度为0.5米.
点评 本题考查了二次函数的应用,涉及了待定系数法求抛物线解析式的知识,注意建立数学模型,培养自己利用数学知识解决实际问题的能力,难度一般.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:选择题
 如图,为估计池塘两岸A、B间的距离,杨阳在池塘一侧选取了一点P,测得PA=16cm,PB=12m,那么A、B间的距离不可能是( )
如图,为估计池塘两岸A、B间的距离,杨阳在池塘一侧选取了一点P,测得PA=16cm,PB=12m,那么A、B间的距离不可能是( )| A. | 10m | B. | 15m | C. | 20m | D. | 29m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
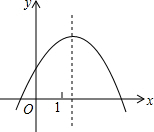 已知函数y=ax2+bx+c的图象如图所示,给出下列不等式:①a<0;②b<0;③c>0;④a+b+c>0,其中正确的有( )个.
已知函数y=ax2+bx+c的图象如图所示,给出下列不等式:①a<0;②b<0;③c>0;④a+b+c>0,其中正确的有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
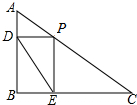 如图,在△ABC中,∠B=90°,AB=15cm,∠A=60°,动点P从点A开始沿AC点向C以2cm/s的速度移动(不与C重合),过点P作PD∥BC交AB于D,过P作PE∥AB交BC于E,若P点运动时间为t s.
如图,在△ABC中,∠B=90°,AB=15cm,∠A=60°,动点P从点A开始沿AC点向C以2cm/s的速度移动(不与C重合),过点P作PD∥BC交AB于D,过P作PE∥AB交BC于E,若P点运动时间为t s.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
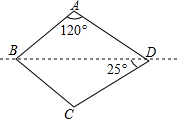 如图,直线BD是四边形ABCD的对称轴,已知∠BAD=120°,∠CDB=25°,则∠ABC的度数为( )
如图,直线BD是四边形ABCD的对称轴,已知∠BAD=120°,∠CDB=25°,则∠ABC的度数为( )| A. | 70° | B. | 60° | C. | 50° | D. | 80° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com