
科目:初中数学 来源: 题型:填空题
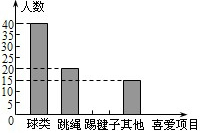 某学校为了解学生大课间体育活动情况,随机抽取本校100名学生进行调查,整理收集到的数据,绘制成如图所示的统计图.若该校共有1000名学生,估计喜欢“踢毽子”的学生有250人.
某学校为了解学生大课间体育活动情况,随机抽取本校100名学生进行调查,整理收集到的数据,绘制成如图所示的统计图.若该校共有1000名学生,估计喜欢“踢毽子”的学生有250人.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
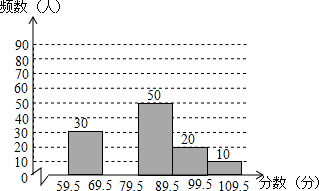 某中学举行了一次“生活中的”知识竞赛,赛后李老师抽取部分参赛同学的成绩(成绩为整数,满分为110分).进行整理,并制成图表(不完整)如下:
某中学举行了一次“生活中的”知识竞赛,赛后李老师抽取部分参赛同学的成绩(成绩为整数,满分为110分).进行整理,并制成图表(不完整)如下:| 分数段 | 频数 | 频率 |
| 第一次:59.5-69.5 | 30 | 0.15 |
| 第二次:69.5-79.5 | 90 | 0.45 |
| 第三次79.5-89.5 | 50 | 0.25 |
| 第四组89.5-99.5 | 20 | 0.1 |
| 第五组99.5-109.5 | 10 | 0.05 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
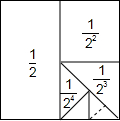 在数学活动中,小明为了求$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$的值(结果用n表示),设计如图所示的几何图形,请你利用这个几何图形求$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$的值为1-$\frac{1}{{2}^{n}}$.
在数学活动中,小明为了求$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$的值(结果用n表示),设计如图所示的几何图形,请你利用这个几何图形求$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$的值为1-$\frac{1}{{2}^{n}}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
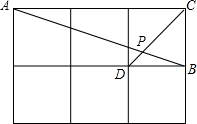 如图,在边长都为1的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,
如图,在边长都为1的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com