
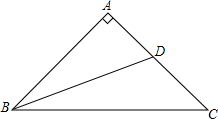
 如图,已知在Rt△ABC中,∠A=90°,AB=BC,BD是AC边上的中线,求cot∠DBC.
如图,已知在Rt△ABC中,∠A=90°,AB=BC,BD是AC边上的中线,求cot∠DBC. 分析 设AB=AC=2x,根据勾股定理求出BC,求出AD=DC=x,∠C=∠ABC=∠EDC=45°,推出DE=CE,解直角三角形求出DE、EC,即可求出答案.
解答 解:如图: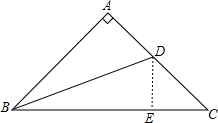
设AB=AC=2x,由勾股定理得:BC=$\sqrt{(2x)^{2}+(2x)^{2}}$=2$\sqrt{2}$x,
则AD=DC=x,
过D作DE⊥BC于E,则∠DEC=90°,
∵在Rt△ABC中,∠A=90°,AB=BC,
∴∠C=∠ABC=45°,
∴∠EDC=∠C=45°,
∴DE=CE,
∴DE=EC=DC×sin45°=$\frac{\sqrt{2}}{2}$x,
∴BE=BC-EC=$\frac{3\sqrt{2}}{2}$x,
在Rt△BED中,cot∠DBC=$\frac{BE}{DE}$=$\frac{\frac{3\sqrt{2}}{2}x}{\frac{\sqrt{2}}{2}x}$=3.
点评 本题考查了解直角三角形,等腰三角形的性质和判定,勾股定理的应用,解此题的关键是能正确作出辅助线,构造直角三角形,是一道比较好的题目,难度适中.


科目:初中数学 来源: 题型:解答题
| 6,8,10 | 8,15,17 | 10,24,26 | … | 20,b,c |
| 62+82=102 | 82+152=172 | 102+242=262 | … | 202+b2=c2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
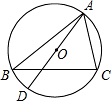 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为$\frac{3}{2}$,AC=2,则sinB的值是( )
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为$\frac{3}{2}$,AC=2,则sinB的值是( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com