
【题目】(1)探究发现:下面是一道例题及解答过程,请补充完整:
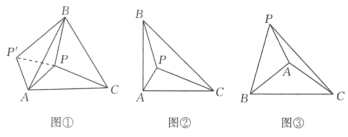
如图①在等边△ABC内部,有一点P,若∠APB=150°,求证:AP2+BP2=CP2
证明:将△APC绕A点逆时针旋转60°,得到△AP’B,连接PP’,则△APP’为等边三角形
∴∠APP’=60° ,PA=PP’ ,PC=
∵∠APB=150°,∴∠BPP’=90°
∴P’P2+BP2= ,即PA2+PB2=PC2
(2)类比延伸:如图②在等腰△ABC中,∠BAC=90°,内部有一点P,若∠APB=135°,试判断线段PA,PB,PC之间的数量关系,并证明.
(3)联想拓展:如图③在△ABC中,∠BAC=120°,AB=AC,点P在直线AB上方,且∠APB=60°,满足(kPA)2+PB2=PC2(其中k>0),请直接写出k的值.
【答案】(1)P’B,P’B2;(2)2PA2+PB2=PC2,见解析;(3)k=![]()
【解析】
(1)根据旋转的性质和勾股定理直接写出即可.
(2)将△APC绕A点逆时针旋转90°,得到△AP′B,连接PP′,论证PP′=2PA,再根据勾股定理代换即可.
(3)将△APC 绕A点顺时针旋转120°得到△AP′B,连接PP′,过点A作AH⊥PP′,论证PP′=![]() PA,再根据勾股定理代换即可.
PA,再根据勾股定理代换即可.
(1)PC=P’B,P’P2+BP2=P’B2
(2)关系式为:2PA2+PB2=PC2
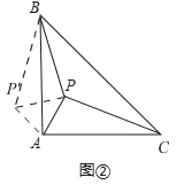
证明:将△APC绕A点逆时针旋转90°,得到△AP’B,连接PP’,则△APP’为等腰直角三角形,
∴∠APP’=45°,PP’=![]() PA,PC=P’B,
PA,PC=P’B,
∵∠APB=135°,
∴∠BPP’=90°,
∴P’P2+BP2=P’B2,
∴2PA2+PB2=PC2.
(3)k=![]()
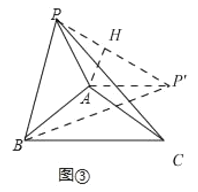
将△APC绕点A顺时针旋转120°得到△AP’B,连接PP’,过点A作AH⊥PP’,
可得![]()
![]()
![]()
![]()
![]()
![]()
![]()


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】2018年湖南省进入高中学习的学生三年后将面对新高考,高考方案与高校招生政策都将有重大变化。某部门为了了解政策的宣传情况,对某初级中学学生进行了随机抽样调查,根据学生对政策的了解程度由高到低分为A,B,C,D四个等级,并对调查结果分析后绘制了如下两幅图不完整的统计图。请你根据图中提供的信息完成下列问题:
(1)求被调查学生的人数,并将条形统计图补充完整;
(2)求扇形统计图中的A等对应的扇形圆心角的度数;
(3)已知该校有1500名学生,估计该校学生对政策内容了解程度达到A等的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如右图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,如果点B的横坐标为x,点C的纵坐标为y,那么表示y与x的函数关系的图像大致是( )
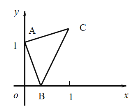
A.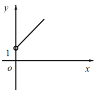 B.
B.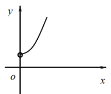
C.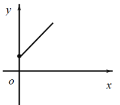 D.
D.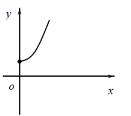
查看答案和解析>>
科目:初中数学 来源: 题型:
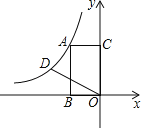
【题目】如图,矩形ABOC的顶点B、C分别在x轴,y轴上,顶点A在第二象限,点B的坐标为(﹣2,0).将线段OC绕点O逆时针旋转60°至线段OD,若反比例函数y=![]() (k≠0)的图象经过A、D两点,则k值为______.
(k≠0)的图象经过A、D两点,则k值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形组成的网格中建立直角坐标系,△AOB的顶点均在格点上,点O为原点,点A、B的坐标分别是A(3,2)、B(1,3).

(1)将△AOB向下平移3个单位后得到△A1O1B1,则点B1的坐标为 ;
(2)将△AOB绕点O逆时针旋转90°后得到△A2OB2,请在图中作出△A2OB2,并求出这时点A2的坐标为 ;
(3)在(2)中的旋转过程中,线段OA扫过的图形的面积 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推出一款新产品,通过市场调研后,按三种颜色受欢迎的程度分别对A颜色、B颜色、C颜色的产品在成本的基础上分别加价40%,50%,60%出售(三种颜色产品的成本一样),经过一个季度的经营后,发现C颜色产品的销量占总销量的40%,三种颜色产品的总利润率为51.5%,第二个季度,公司决定对A产品进行升级,升级后A产品的成本提高了25%,其销量提高了60%,利润率为原来的两倍;B产品的销量提高到与升级后的A产品的销量一样,C产品的销量比第一季度提高了50%,则第二个季度的总利润率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在开展“经典阅读”活动中,某学校为了解全校学生利用课外时间阅读的情况,学校团委随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计表.根据图表信息,解答下列问题:
频率分布表
阅读时间(小时) | 频数(人) | 频率 |
| 6 | 0.12 |
|
| 0.24 |
| 15 | 0.3 |
| 12 |
|
| 5 | 0.1 |
合计 |
| 1 |
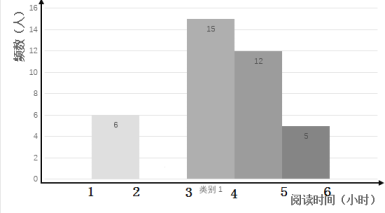
(1)求![]() __________,
__________,![]() _________;
_________;
(2)将频数分布直方图补充完整(画图后请标注相应的频数);
(3)在![]() 范围内的5名同学中恰好有2名男生和3名女生,现从中随机挑选2名同学代表学校参加全市经典阅读比赛,请用树状图法或者列表法求出恰好选中“1男1女”的概率.
范围内的5名同学中恰好有2名男生和3名女生,现从中随机挑选2名同学代表学校参加全市经典阅读比赛,请用树状图法或者列表法求出恰好选中“1男1女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第36届全国信息学冬令营在广州落下帷幕,长郡师生闪耀各大赛场,金牌数、奖牌数均稳居湖南省第一.学校拟预算7700元全部用于购买甲、乙、丙三种图书共20套奖励获奖师生,其中甲种图书每套500元,乙种图书每套400元,丙种图书每套250元,设购买甲种图书x套,乙种图书y套,请解答下列问题:
(1)请求出y与x的函数关系式(不需要写出自变量的取值范围);
(2)若学校购买的甲、乙两种图书共14套,求甲、乙图书各多少套?
(3)若学校购买的甲、乙两种图书均不少于1套,则有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把八个完全相同的小球平分为两组,每组中每个分别写上1,2,3,4四个数字,然后分别装入不透明的口袋内搅匀,从第一个口袋内取出一个数记下数字后作为点P的横坐标x,然后再从第二个口袋中取出一个球记下数字后作为点P的纵坐标,则点P(x,y)落在直线y=﹣x+5上的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com