
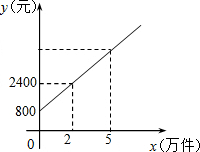
 某公司市场营销部的某营销员的个人月收入与该营销员每月的销售量成一次函数关系,其图象如图所示,根据图象提供的信息,解答下列问题:
某公司市场营销部的某营销员的个人月收入与该营销员每月的销售量成一次函数关系,其图象如图所示,根据图象提供的信息,解答下列问题:分析 (1)设y=kx+b,将(0,800)与(2,2400)代入,利用待定系数法即可求解;
(2)设这个增长率为x,先根据(1)中所求的解析式求出x=5时对应的y值,再由两个月内该营销员的销售量从2万件猛增到5万件,且连续两个月的月收入的增长率是相同的列出方程,解方程即可.
解答 解:(1)设y=kx+b,将(0,800)与(2,2400)代入,
得$\left\{\begin{array}{l}{b=800}\\{2k+b=2400}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=800}\\{b=800}\end{array}\right.$,
故营销员的个人月收入y元与该营销员每月的销售量x万件(x≥0)之间的函数关系式为y=800x+800;
(2)∵y=800x+800,
∴当x=5时,y=800×5+800=4800.
设这个增长率为x,根据题意得
2400(1+x)2=4800,
解得x1=$\sqrt{2}$-1≈0.41,x2=-$\sqrt{2}$-1(不合题意舍去).
答:这个增长率约为41%.
点评 本题考查一元二次方程的应用,判断所求的解是否符合题意,舍去不合题意的解.找到关键描述语,找到等量关系准确的列出方程是解决问题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com