
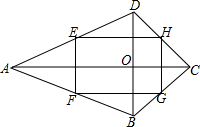
 如图,在四边形ABCD中,AC⊥DB,垂足为O,点E、F、G、H分别为AD、AB、BC、CD的中点,求证:四边形EFGH是矩形.
如图,在四边形ABCD中,AC⊥DB,垂足为O,点E、F、G、H分别为AD、AB、BC、CD的中点,求证:四边形EFGH是矩形.  学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:解答题
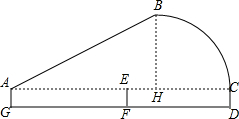 小明代表学校在邵阳市羽毛球比赛中,击出如图所示的球,其中A-B-C-D代表球飞行的弧度,经测量,小明同学击球时站在距离球网5m的G处,球网在点F处,而球落在球网对面的D处,DF=5m,击出球的角度约为30°,小明的击球高度约为1.6米,近似地把BC段看成$\frac{1}{4}$的圆,∠BHC=90°.比赛完后,小明想知道该球飞行的路程(即线段AB-C-D长)与球最高点B的高度,请你运用所学的知识帮他计算以下.($\sqrt{3}$≈1.73,π≈3.14,结果精确到0.1m)
小明代表学校在邵阳市羽毛球比赛中,击出如图所示的球,其中A-B-C-D代表球飞行的弧度,经测量,小明同学击球时站在距离球网5m的G处,球网在点F处,而球落在球网对面的D处,DF=5m,击出球的角度约为30°,小明的击球高度约为1.6米,近似地把BC段看成$\frac{1}{4}$的圆,∠BHC=90°.比赛完后,小明想知道该球飞行的路程(即线段AB-C-D长)与球最高点B的高度,请你运用所学的知识帮他计算以下.($\sqrt{3}$≈1.73,π≈3.14,结果精确到0.1m)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
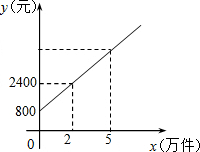 某公司市场营销部的某营销员的个人月收入与该营销员每月的销售量成一次函数关系,其图象如图所示,根据图象提供的信息,解答下列问题:
某公司市场营销部的某营销员的个人月收入与该营销员每月的销售量成一次函数关系,其图象如图所示,根据图象提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
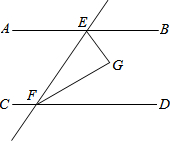 如图,直线AB、CD被直线EF所截,EG平分∠BEF,FG平分∠DFE,已知∠AEF=60°-x°,∠CFE=120°+x°.
如图,直线AB、CD被直线EF所截,EG平分∠BEF,FG平分∠DFE,已知∠AEF=60°-x°,∠CFE=120°+x°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 十六进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 十进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| A. | 72 | B. | 6E | C. | 5F | D. | B0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com