
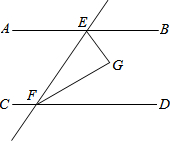
 如图,直线AB、CD被直线EF所截,EG平分∠BEF,FG平分∠DFE,已知∠AEF=60°-x°,∠CFE=120°+x°.
如图,直线AB、CD被直线EF所截,EG平分∠BEF,FG平分∠DFE,已知∠AEF=60°-x°,∠CFE=120°+x°.分析 (1)求出∠AEF+∠CFE=180°,根据平行线的判定得出即可;
(2)求出∠CFE的度数,求出∠DFE,根据角平分线定义求出即可;
(3)根据平行线的性质求出∠BEF+∠DFE=180°,根据角平分线定义得出∠GEF=$\frac{1}{2}$∠BEF,∠GFE=$\frac{1}{2}$∠DFE,求出∠GEF+∠GFE=90°,根据三角形内角和定理求出∠G即可.
解答 解:(1)AB∥CD,
理由是:∵∠AEF=60°-x°,∠CFE=120°+x°,
∴∠AEF+∠CFE=180°,
∴AB∥CD;
(2)∵当x=10时,∠CFE=120°-10°=110°,
∴∠DFE=180°-110°=70°°,
∵FG平分∠DFE,
∴∠EFG=$\frac{1}{2}$∠DFE=35°;
(3)EG⊥FG,
理由是:∵AB∥CD,
∴∠BEF+∠DFE=180°,
∵EG平分∠BEF,FG平分∠DFE,
∴∠GEF=$\frac{1}{2}$∠BEF,∠GFE=$\frac{1}{2}$∠DFE,
∴∠GEF+∠GFE=90°,
∴∠G=180°-(∠GEF+∠∠GFE)=90°,
∴EG⊥FG.
点评 本题考查了平行线的性质和判定,三角形内角和定理,垂直定义,角平分线定义的应用,能正确运用定理进行推理是解此题的关键,注意:同旁内角互补,两直线平行,反之亦然.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 用一根长为a m的篱笆在空地上围一绿化场地,现有两种方案:
用一根长为a m的篱笆在空地上围一绿化场地,现有两种方案:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com