
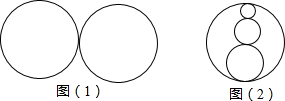
分析 (1)设大圆直径为d,周长为l,图(2)中三个小圆的直径分别是d1,d2,d3,周长分别是l1,l2,l3,根据圆的周长公式得到l=πd=π(d1+d2+d3)=l1+l2+l3,于是可判断两种方案所用材料一样多;
(2)说理的方法与(1)一样.
解答 解:(1)大圆直径为d,周长为l,图(2)中三个小圆的直径分别是d1,d2,d3,周长分别是l1,l2,l3,
l=πd=π(d1+d2+d3)=πd1+πd2+πd3=l1+l2+l3,
则图(1)中一个大圆周长与图(2)中三个小圆周长的和相等,即两种方案所用材料一样多;
(2)将三个小圆改成n个小圆,结论成立.理由如下:
设大圆直径为d,周长为l,n个小圆的直径分别是d1,d2,…,dn,周长分别是l1,l2,…,ln,
则l=πd=π(d1+d2+…+dn)=πd1+πd2+…+πdn=l1+l2+…+ln,
所以图(1)中一个大圆周长与n个小圆周长的和相等,即两种方案所用材料一样多.
点评 本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).


科目:初中数学 来源: 题型:填空题
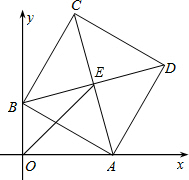 已知边长为a的正方形ABCD,两顶点A、B分别在平面直角坐标系的x轴、y轴的正半轴上滑动,点C点D在第一象限,点E为正方形ABCD的对称中心,连结OE,则OE的长的最大值是a.
已知边长为a的正方形ABCD,两顶点A、B分别在平面直角坐标系的x轴、y轴的正半轴上滑动,点C点D在第一象限,点E为正方形ABCD的对称中心,连结OE,则OE的长的最大值是a.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{3}}{3}$R,R,$\sqrt{3}$R2 | B. | R,$\frac{R}{2}$,2$\sqrt{3}$R2 | C. | $\frac{\sqrt{3}}{3}$R,R,2$\sqrt{3}$R2 | D. | R,$\frac{\sqrt{3}}{2}$R,$\frac{{3\sqrt{3}}}{2}{R^2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
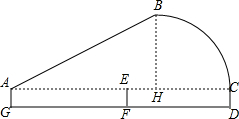 小明代表学校在邵阳市羽毛球比赛中,击出如图所示的球,其中A-B-C-D代表球飞行的弧度,经测量,小明同学击球时站在距离球网5m的G处,球网在点F处,而球落在球网对面的D处,DF=5m,击出球的角度约为30°,小明的击球高度约为1.6米,近似地把BC段看成$\frac{1}{4}$的圆,∠BHC=90°.比赛完后,小明想知道该球飞行的路程(即线段AB-C-D长)与球最高点B的高度,请你运用所学的知识帮他计算以下.($\sqrt{3}$≈1.73,π≈3.14,结果精确到0.1m)
小明代表学校在邵阳市羽毛球比赛中,击出如图所示的球,其中A-B-C-D代表球飞行的弧度,经测量,小明同学击球时站在距离球网5m的G处,球网在点F处,而球落在球网对面的D处,DF=5m,击出球的角度约为30°,小明的击球高度约为1.6米,近似地把BC段看成$\frac{1}{4}$的圆,∠BHC=90°.比赛完后,小明想知道该球飞行的路程(即线段AB-C-D长)与球最高点B的高度,请你运用所学的知识帮他计算以下.($\sqrt{3}$≈1.73,π≈3.14,结果精确到0.1m)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
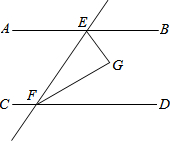 如图,直线AB、CD被直线EF所截,EG平分∠BEF,FG平分∠DFE,已知∠AEF=60°-x°,∠CFE=120°+x°.
如图,直线AB、CD被直线EF所截,EG平分∠BEF,FG平分∠DFE,已知∠AEF=60°-x°,∠CFE=120°+x°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com