
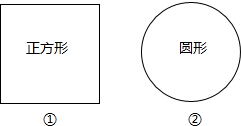
 用一根长为a m的篱笆在空地上围一绿化场地,现有两种方案:
用一根长为a m的篱笆在空地上围一绿化场地,现有两种方案:分析 根据周长求出正方形的边长,再根据面积公式,正方形的面积=边长×边长计算即可,再根据周长求出圆的半径,然后根据S=πr2计算即可,进而比较两种不同图形面积的大小即可.
解答 解:围成圆形场地面积较大.
理由:设正方形的边长为b米,则4b=a,
∴b=$\frac{a}{4}$米,
∴正方形的面积=$\frac{a}{4}$×$\frac{a}{4}$=$\frac{{a}^{2}}{16}$(平方米);
∵2πr=a,∴r=$\frac{a}{2π}$,
∴S=πr2=π×$\frac{{a}^{2}}{4{π}^{2}}$=$\frac{{a}^{2}}{4π}$(平方米);
∵16>4π,
∴$\frac{{a}^{2}}{16}$<$\frac{{a}^{2}}{4π}$.
∴围成圆形场地面积较大.
点评 本题考查了列代数式、有理数的混合运算,用到的知识点:正方形的面积=边长×边长,S=πr2,牢记公式是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
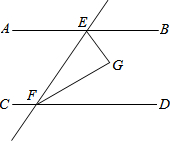 如图,直线AB、CD被直线EF所截,EG平分∠BEF,FG平分∠DFE,已知∠AEF=60°-x°,∠CFE=120°+x°.
如图,直线AB、CD被直线EF所截,EG平分∠BEF,FG平分∠DFE,已知∠AEF=60°-x°,∠CFE=120°+x°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 十六进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 十进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| A. | 72 | B. | 6E | C. | 5F | D. | B0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com