
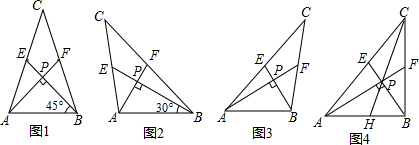
分析 (1)由∠ABE=45°,c=2$\sqrt{2}$,得到AP=BP=2,由$\frac{PE}{PB}=\frac{PF}{PA}=\frac{EF}{AB}=\frac{1}{2}$ 求出PE,PF即可;
(2)设PF=m,PE=n,由 $\frac{PE}{PB}=\frac{PF}{PA}=\frac{1}{2}$得到AP=2m,PB=2n,再由勾股定理即可;
(3)判断出△ABF是“中垂三角形”,利用(2)结论得出AC2+BC2=5BA2求出BA即可.
解答 解:如图1.连接EF,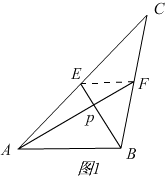
∵AE,AF是△ABC的中线,
∴AF⊥BE,
当∠ABE=45°,c=2$\sqrt{2}$时
在Rt△APB中,AB=c=2$\sqrt{2}$,∠ABE=45°
∴AP=BP=2.
∵AE,AF是△ABC的中线,
∴EF∥AB,
∴$\frac{PE}{PB}=\frac{PF}{PA}=\frac{EF}{AB}=\frac{1}{2}$
∴PE=PF=1,
在Rt△APE中,AP=2,PE=1,
∴AE=$\sqrt{{AP}^{2}{+PE}^{2}}$=$\sqrt{5}$,
∴b=a=2AE=2$\sqrt{5}$,
当∠ABE=30°,c=4时
在Rt△APB中,AB=c=4,∠ABE=30°,
∴AP=$\frac{1}{2}$AB=2,PB=2$\sqrt{3}$,
∵EF∥BC,
∴$\frac{PE}{PB}=\frac{PF}{PA}=\frac{1}{2}$,
∴PE=$\sqrt{3}$,PF=1,
在Rt△APE中,AE=$\sqrt{{PA}^{2}{+PE}^{2}}$=$\sqrt{7}$,
∴b=AC=2AE=2$\sqrt{7}$,
同理:a=BC=2BF=2$\sqrt{13}$
故答案为2$\sqrt{5}$,2$\sqrt{5}$,2$\sqrt{13}$,2$\sqrt{7}$;
(2)如图1,连接EF,
∵AF,BE是△ABC的中线,
∴EF是△ABC的中位线,
∴EF∥AB,且EF=$\frac{1}{2}$AB=$\frac{1}{2}$c,
∴$\frac{PE}{PB}=\frac{PF}{PA}=\frac{1}{2}$,
设PF=m,PE=n,
∴AP=2m,PB=2n,
在Rt△APB中,(2m)2+(2n)2=c2
在Rt△APE中,(2m)2+n2=($\frac{b}{2}$)2,
在Rt△FPB中,m2+(2n)2=($\frac{a}{2}$)2,
∴a2+b2=5c2;
(3)∵AF,BE是△ABC的中线,AF⊥BE
∴△ABC是“中垂三角形”,
∴AC2+BC2=5BA2,
∵AC=7cm,BC=6cm
∴72+62=5BA2,
∴AB=$\sqrt{17}$;
在Rt△APB中,PH=$\frac{1}{2}$AB=$\frac{\sqrt{17}}{2}$.
点评 此题是相似形综合题,主要考查了勾股定理得应用,和“中垂三角形”定义,根据条件表示相关的线段是解本题的关键.


 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:初中数学 来源: 题型:解答题
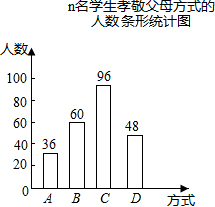 某校团委为了了解学生孝敬父母的情况,在全校范围内随机抽取n名学生进行问卷调查.问卷中孝敬父母方式包括:A.为父母洗一次脚;B.帮父母做一次家务;C.给父母买一件礼物;D.其他.每位学生在问卷调查时都按要求只选择了其中一种方式,该校团委收回全部问卷后,将收集到的数据整理并绘制成如下的统计图.
某校团委为了了解学生孝敬父母的情况,在全校范围内随机抽取n名学生进行问卷调查.问卷中孝敬父母方式包括:A.为父母洗一次脚;B.帮父母做一次家务;C.给父母买一件礼物;D.其他.每位学生在问卷调查时都按要求只选择了其中一种方式,该校团委收回全部问卷后,将收集到的数据整理并绘制成如下的统计图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
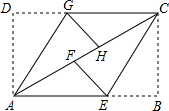 如图,ABCD是矩形纸片,翻折∠B、∠D,使点B、D恰好落在AC边上的点F、H处,CE与AG为折痕.
如图,ABCD是矩形纸片,翻折∠B、∠D,使点B、D恰好落在AC边上的点F、H处,CE与AG为折痕.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com