练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．用一些三角形纸片铺在桌面上（小的三角形覆盖在大的三角形上），组成下面的图形：
    第10个图形需要三角形纸片100张，第n个图形需要三角形纸片n2张．

    分析 由图可知：第一个图形有1=12个小三角形纸片；第二个图形有1+3=4=22个小三角形纸片；第三个图形有1+3+5=9=32个小三角形纸片；第四个图形有1+3+5+7=16=42个小三角形纸片；…以此类推，可知第n个图形中需要n2个小三角形纸片，进一步代入求得答案即可．

    解答 解：∵第一个图形有1=12个小三角形纸片；
    第二个图形有1+3=4=22个小三角形纸片；
    第三个图形有1+3+5=9=32个小三角形纸片；
    第四个图形有1+3+5+7=16=42个小三角形纸片；
    …
    ∴第n个图形中需要n2个小三角形纸片．
    ∴第10个图形需要三角形纸片100张，第n个图形需要三角形纸片n2张．
    故答案为：100，n2．

    点评 此题考查图形的变化规律，找出图形之间的联系，得出数字的运算规律解决问题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    6．已知直线l与直线y=2x+1交点的横坐标为1，与直线y=-x-8交点的纵坐标为-8，求直线l的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．若代数式5x2-2mxy-3y2+4xy-3x+1中不含xy项，求（-m3+2m2-m+1）-（m3+2m2-m+4）的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

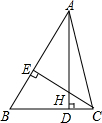    10．如图，在△ABC中，AD⊥BC，CE⊥AB，垂足分别为D，E，AD，CE交于一点H，已知EH=EB=9，AE=12，则CH的长是（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．已知：如图，AD、BC相交于点O，且AD=BC，∠C=∠D=90°．
    （1）求证：Rt△ABC≌Rt△BAD；
    （2）求证：CO=DO．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

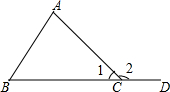    7．已知，如图，∠2是△ABC的一个外角，求证：∠2=∠A+∠B．
    证明：如图，∵∠A+∠B+∠1=180°（三角形内角和定理）
    ∠1+∠2=180°（平角的定义）
    ∴∠2=∠A+∠B（等量代换）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

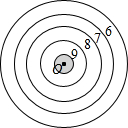    14．如图所示，小明在劳动课上做了一个靶子，靶心圆的半径为2cm，击中为10环（阴影部分），向外依次是9，8，7，6环，10，9，8，7，6圆环间距离都是3cm．
    （1）求7环的内环、外环圆的半径；
    （2）若某射击手击中点A，点A距靶心O为12.8cm，他的成绩是几环？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．如图，AD、BC是⊙O的两条互相垂直的直径，点P从O点出发，沿0CDO的路线匀速运动，设点P运动的时间为x（单位：秒），∠APB=y（单位：度），那么表示y与x之间关系的图象是（　　）
    A．B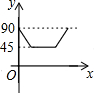．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图1，P（2，2），点A在x轴正半轴上运动，点B在y轴负半轴上运动，且PA=PB．
    （1）求证：PA⊥PB；
    （2）若点A（8，0），求点B的坐标；
    （3）求OA-OB的值；
    （4）如图2，若点B在y轴正半轴上运动时，直接写出OA+OB的值．

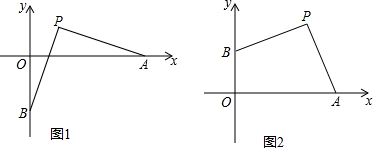
    查看答案和解析>>

    同步练习册答案