
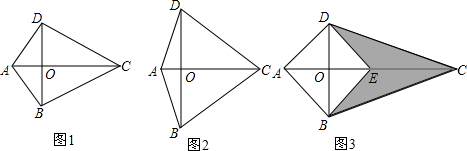
���� ��1���������εĶ���ɵ����ʣ���������һ��Խ���ȣ���������һ���Խ��ߴ�ֱƽ����һ���Խ��ߣ���������һ���Խ���ƽ��һ��Խǣ��ж�������һ���Խ��ߴ�ֱƽһ���Խ��ߵ��ı��������Σ�����һ���Խ���ƽ��һ��Խǵ��ı��������Σ����ݶ���õ�AD=AB��CD=CB��֤����ADC=��ABC����ȫ�������μ��ɵõ����ۣ��ж�����ͼ1����A���ı���ABCD�ĶԽ��ߣ�ACƽ�֡�DAB�͡�DCB��֤���ı���ABCD�����Σ�ͨ����ADC�ա�ABC������֤�ý��ۣ�
��2������OC=2OD=2OB=a����CD=BD=$\sqrt{5}$a����S��BCD=$\frac{1}{2}$CD•CBsin��BCD=$\frac{1}{2}$BD•CD���õ�����$\frac{1}{2}$��$\sqrt{5}$a��2sin��BCD=$\frac{1}{2}$��2a��2a���ɵ�sin��BCD=$\frac{4}{5}$����tan��BCD=$\frac{4}{3}$��
����ͼ2������BDC��ƽ���߽�AC�ڵ�E���ڡ�BCD=72�㣬�õ���2=$\frac{1}{2}$��BCD=36�㣬�ɡ�DAC=72�㣬�õ���ADC=72�㣬��1=36�Ƴ���DAE�ס�CDA�õ�����ʽ$\frac{AD}{AE}=\frac{DC}{DA}$��DC=AC��AE=AC-CE=CD-AD���ۿɵã�
��3�������AOD�У�һ���ڽ�����һ���ڽǵ�2����������������ٵ���AOD=2��DAO�����۵������ʵ�DB��AE��AO=OE���õ�������AOD�ǵ���ֱ�������Σ�����Ӱ����ͼ�ε���������ı���ABED��������õ�AE=CE��OC=3AO=3OD���ɹ��ɶ����õ�CD=$\sqrt{{OD}^{2}+��3OD��^{2}}$=$\sqrt{10}OD$�����$\frac{AD}{CD}$=$\frac{\sqrt{2}OD}{\sqrt{10}OD}$=1��$\sqrt{5}$���ڵ���DAO=2��ADO����á�DAO=60�㣬��AD0=30�㣬�õ�AD=$\frac{2\sqrt{3}}{3}$OD��AO=$\frac{\sqrt{3}}{3}OD$������AE=CE��OC=3AO=$\sqrt{3}$OD���ɹ��ɶ����õ�CD=$\sqrt{O{D}^{2}+O{C}^{2}}$=2OD�����ǵõ�����$\frac{AD}{CD}$=$\frac{\frac{2\sqrt{3}}{3}OD}{2OD}$=1��$\sqrt{3}$���۵���ADO=2��DAO���õ���ADO=60�㣬��DAO=30�㣬���ǵõ�AD=2OD��AO=$\sqrt{3}$OD������AE=CE��OC=3AO=3$\sqrt{3}$OD���ɹ��ɶ����õ�CD=$\sqrt{O{D}^{2}++O{C}^{2}}$=2$\sqrt{7}$OD�����ǵõ�����$\frac{AD}{CD}$=$\frac{2OD}{2\sqrt{7}OD}$=1��$\sqrt{7}$��
���  �⣺��1�����ʣ���������һ��Խ���ȣ�
�⣺��1�����ʣ���������һ��Խ���ȣ�
��������һ���Խ��ߴ�ֱƽ����һ���Խ��ߣ�
��������һ���Խ���ƽ��һ��Խǣ�
�ж�������һ���Խ��ߴ�ֱƽ����һ���Խ��ߵ��ı��������Σ�
����һ���Խ���ƽ��һ��Խǵ��ı��������Σ�
֤�����£����ʢ���ͼ1����֪AD=AB��CD=CB����֤����ADC=��ABC��
֤�����ڡ�ADC���ABC�У�
$\left\{\begin{array}{l}{AD=AB}\\{CD=BC}\\{AC=AC}\end{array}\right.$��
���ADC�ա�ABC��
���ADC=��ABC��
�ж�����ͼ1����֪AC���ı���ABCD�ĶԽ��ߣ�ACƽ�֡�DAB�͡�DCB����֤���ı���ABCD�����Σ�
֤������ACƽ�֡�DAB�͡�DCB��
���DAC=��BAC����DCA=��BCA��
�ڡ�ADC���ABC�У�
$\left\{\begin{array}{l}{��DAC=��BAC}\\{AC=AC}\\{��DCA=��BCA}\end{array}\right.$��
���ADC�ա�ABC��
��AD=AB��BC=CD��
���ı���ABCD�����Σ�
��2������OC=2OD=2OB=a����CD=BD=$\sqrt{5}$a��
��S��BCD=$\frac{1}{2}$CD•CBsin��BCD=$\frac{1}{2}$BD•CD��
��$\frac{1}{2}$��$\sqrt{5}$a��2sin��BCD=$\frac{1}{2}$��2a��2a��
�ɵã�sin��BCD=$\frac{4}{5}$����tan��BCD=$\frac{4}{3}$��
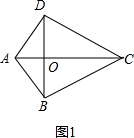
����ͼ2������BDC��ƽ���߽�AC�ڵ�E��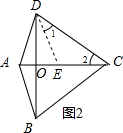
�ߡ�BCD=72�㣬
���2=$\frac{1}{2}$��BCD=36�㣬
�ߡ�DAC=72�㣬
���ADC=72�㣬��1=36��
���DAE�ס�CDA
��$\frac{AD}{AE}=\frac{DC}{DA}$��DC=AC��AE=AC-CE=CD-AD
����$\frac{AD}{CD-AD}=\frac{CD}{AD}$��
ȥ��ĸ�ã�AD2+CD•AD-CD2=0��
���$AD=\frac{{-1+\sqrt{5}}}{2}CD$��$AD=\frac{{-1-\sqrt{5}}}{2}CD$����ȥ����
��AD��CD=$\frac{{-1+\sqrt{5}}}{2}$��
��3���������AOD�У�һ���ڽ�����һ���ڽǵ�2����
�ٵ���AOD=2��DAO��
���۵������ʵ�DB��AE��AO=OE��
���DAO=45�㣬
��AD=$\sqrt{2}$OD��AO=OD
����Ӱ����ͼ�ε���������ı���ABED�������
��AE=CE��OC=3AO=3OD��
��CD=$\sqrt{{OD}^{2}+��3OD��^{2}}$=$\sqrt{10}OD$��
��$\frac{AD}{CD}$=$\frac{\sqrt{2}OD}{\sqrt{10}OD}$=1��$\sqrt{5}$��
�ڵ���DAO=2��ADO��
���DAO=60�㣬��AD0=30�㣬
��AD=$\frac{2\sqrt{3}}{3}$OD��AO=$\frac{\sqrt{3}}{3}OD$��
��AE=CE��OC=3AO=$\sqrt{3}$OD��
��CD=$\sqrt{O{D}^{2}+O{C}^{2}}$=2OD��
��$\frac{AD}{CD}$=$\frac{\frac{2\sqrt{3}}{3}OD}{2OD}$=1��$\sqrt{3}$��
�۵���ADO=2��DAO��
���ADO=60�㣬��DAO=30�㣬
��AD=2OD��AO=$\sqrt{3}$OD��
��AE=CE��OC=3AO=3$\sqrt{3}$OD��
��CD=$\sqrt{O{D}^{2}++O{C}^{2}}$=2$\sqrt{7}$OD��
��$\frac{AD}{CD}$=$\frac{2OD}{2\sqrt{7}OD}$=1��$\sqrt{7}$��
���������������AOD�У�һ���ڽ�����һ���ڽǵ�2��������Ӱ����ͼ�ε���������ı���ABED�������$\frac{AD}{CD}$��ֵΪ��1��$\sqrt{5}$��1��$\sqrt{3}$��1��$\sqrt{7}$��
���� ���⿼����ȫ�������ε��ж������ʣ����ɶ��������Ǻ��������������ε����ʣ�ֱ�������ε����ʣ�ע�����˼���Ӧ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2016-2017ѧ�꽭��ʡ���꼶��ѧ�ڵ�һ�ο��õ�����ѧ�Ծ��������棩 ���ͣ���ѡ��
���ж���ʽ��ˣ�������ƽ���ʽ������� ( )
A. 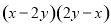 B.
B. 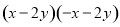
C. 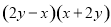 D.
D. 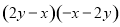
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
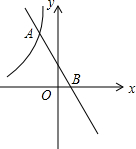 ��ͼ��һ�κ���y2=-2x+b��bΪ��������ͼ���뷴��������y1=$\frac{k}{x}$��kΪ��������k��0����ͼ����A��B���㣬�ҵ�A������Ϊ��-1��4������y1��y2ʱ����x��ȡֵ��Χ��
��ͼ��һ�κ���y2=-2x+b��bΪ��������ͼ���뷴��������y1=$\frac{k}{x}$��kΪ��������k��0����ͼ����A��B���㣬�ҵ�A������Ϊ��-1��4������y1��y2ʱ����x��ȡֵ��Χ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| A������ | B������ | |
| �� | 200 | 170 |
| �ҵ� | 160 | 150 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
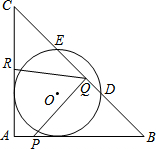 ��ͼ���ڡ�ABC�У���A=90�㣬AB=AC=12cm���뾶Ϊ4cm�ġ�O��AB��AC���߶����У���BC���ڵ�D��E����P�ӵ�A���������ű�AB���յ�B�˶�����Q�ӵ�B���������ű�BC���յ�C�˶�����R�ӵ�C���������ű�CA���յ�A�˶�����֪��P��Q��Rͬʱ�������˶��ٶȷֱ���1cm/s��xcm/s��1.5cm/s���˶�ʱ��Ϊts��
��ͼ���ڡ�ABC�У���A=90�㣬AB=AC=12cm���뾶Ϊ4cm�ġ�O��AB��AC���߶����У���BC���ڵ�D��E����P�ӵ�A���������ű�AB���յ�B�˶�����Q�ӵ�B���������ű�BC���յ�C�˶�����R�ӵ�C���������ű�CA���յ�A�˶�����֪��P��Q��Rͬʱ�������˶��ٶȷֱ���1cm/s��xcm/s��1.5cm/s���˶�ʱ��Ϊts���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
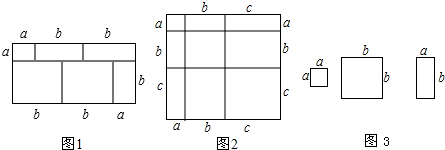
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
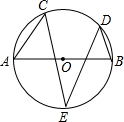 ��ͼ��AB�ǡ�O��ֱ����C��D��E���ǡ�O�ϵĵ㣬��A=55�㣬��B=70�㣬���E�Ķ�����35�㣮
��ͼ��AB�ǡ�O��ֱ����C��D��E���ǡ�O�ϵĵ㣬��A=55�㣬��B=70�㣬���E�Ķ�����35�㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com