
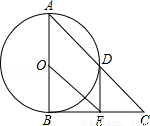
如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心,OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)求证:BC2=2CD•OE;
(3)若cos∠BAD=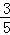 ,BE=
,BE=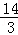 ,求OE的长.
,求OE的长.
(1)DE为⊙O的切线,理由见解析
(2)证明见解析
(3)OE=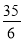
【解析】
试题分析:(1)连接OD,BD,由直径所对的圆周角是直角得到∠ADB为直角,可得出△BCD为直角三角形,E为斜边BC的中点,由直角三角形斜边上的中线等于斜边的一半,得到CE=DE,从而得∠C=∠CDE,再由OA=OD,得∠A=∠ADO,由Rt△ABC中两锐角互余,从而可得∠ADO与∠CDE互余,可得出∠ODE为直角,即DE垂直于半径OD,可得出DE为⊙O的切线;
(2)由已知可得OE是△ABC的中位线,从而有AC=2OE,再由∠C=∠C,∠ABC=∠BDC,可得△ABC∽△BDC,根据相似三角形的对应边的比相等,即可证得;
(3)在直角△ABC中,利用勾股定理求得AC的长,根据三角形中位线定理OE的长即可求得.
试题解析:(1)DE为⊙O的切线,理由如下:
连接OD,BD,
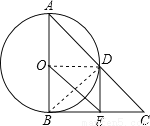
∵AB为⊙O的直径,
∴∠ADB=90°,
在Rt△BDC中,E为斜边BC的中点,
∴CE=DE=BE=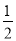 BC,
BC,
∴∠C=∠CDE,
∵OA=OD,
∴∠A=∠ADO,
∵∠ABC=90°,
∴∠C+∠A=90°,
∴∠ADO+∠CDE=90°,
∴∠ODE=90°,
∴DE⊥OD,又OD为圆的半径,
∴DE为⊙O的切线;
(2)∵E是BC的中点,O点是AB的中点,
∴OE是△ABC的中位线,
∴AC=2OE,
∵∠C=∠C,∠ABC=∠BDC,
∴△ABC∽△BDC,
∴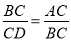 ,即BC2=AC•CD.
,即BC2=AC•CD.
∴BC2=2CD•OE;
(3)【解析】
∵cos∠BAD=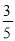 ,
,
∴sin∠BAC=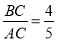 ,
,
又∵BE=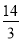 ,E是BC的中点,即BC=
,E是BC的中点,即BC=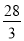 ,
,
∴AC=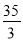 .
.
又∵AC=2OE,
∴OE=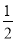 AC=
AC=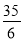 .
.
考点:1、切线的判定;2、相似三角形的判定与性质;3、三角函数


科目:初中数学 来源:2014年初中毕业升学考试(四川达州卷)数学(解析版) 题型:解答题
四张背面完全相同的纸牌(如图,用①、②、③、④表示),正面分别写有四个不同的条件.小明将这4张纸牌背面朝上洗匀后,先随机抽出一张(不放回),再随机抽出一张.

(1)写出两次摸牌出现的所有可能的结果(用①、②、③、④表示);
(2)以两次摸出的牌面上的结果为条件,求能判断四边形ABCD为平行四边形的概率.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川眉山卷)数学(解析版) 题型:选择题
如图,AB、AC是⊙O的两条弦,∠BAC=25°,过点C的切线与OB的延长线交于点D,则∠D的度数为( )
A.25° B.30° C.35° D.40°

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川成都卷)数学(解析版) 题型:解答题
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为192m2,求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川德阳卷)数学(解析版) 题型:选择题
如图所示,边长为2的正三角形ABO的边OB在x轴上,将△ABO绕原点O逆时针旋转30°得到三角形OA1B1,则点A1的坐标为( )

A.( ,1) B.(
,1) B.( ,﹣1) C.(1,﹣
,﹣1) C.(1,﹣ ) D.(2,﹣1)
) D.(2,﹣1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com