四张背面完全相同的纸牌（如图，用①、②、③、④表示），正面分别写有四个不同的条件．小明将这4张纸牌背面朝上洗匀后，先随机抽出一张（不放回），再随机抽出一张．
（1）写出两次摸牌出现的所有可能的结果（用①、②、③、④表示）；
（2）以两次摸出的牌面上的结果为条件，求能判断四边形ABCD为平行四边形的概率．
举一反三期末百分冲刺卷系列答案科目：初中数学 来源：2014年初中毕业升学考试（山东济宁卷）数学（解析版） 题型：解答题
如图，正方形AEFG的顶点E、G在正方形ABCD的边AB、AD上，连接BF、DF.
（1）求证：BF=DF；
（2）连接CF，请直接写出BE∶CF的值（不必写出计算过程）.
查看答案和解析>>
科目：初中数学 来源：2014年初中毕业升学考试（四川雅安卷）数学（解析版） 题型：解答题
如图，⊙O的直径CD垂直于弦AB，垂足为E，F为DC延长线上一点，且∠CBF=∠CDB．
（1）求证：FB为⊙O的切线；
（2）若AB=8，CE=2，求sin∠F．
查看答案和解析>>
科目：初中数学 来源：2014年初中毕业升学考试（四川达州卷）数学（解析版） 题型：解答题
倡导研究性学习方式，着力教材研究，习题研究，是学生跳出题海，提高学习能力和创新能力的有效途径．下面是一案例，请同学们认真阅读、研究，完成“类比猜想”及后面的问题．
习题解答：
习题 如图（1），点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，则EF=BE+DF，说明理由．
解答：∵正方形ABCD中，AB=AD，∠BAD=∠ADC=∠B=90°，
∴把△ABE绕点A逆时针旋转90°至△ADE′，点F、D、E′在一条直线上．
∴∠E′AF=90°﹣45°=45°=∠EAF，
又∵AE′=AE，AF=AF
∴△AE′F≌△AEF（SAS）
∴EF=E′F=DE′+DF=BE+DF．
习题研究
观察分析：观察图（1），由解答可知，该题有用的条件是①ABCD是四边形，点E、F分别在边BC、CD上；②AB=AD；③∠B=∠D=90°；④∠EAF=
∠BAD．
类比猜想：（1）在四边形ABCD中，点E、F分别在BC、CD上，当AB=AD，∠B=∠D时，还有EF=BE+DF吗？
研究一个问题，常从特例入手，请同学们研究：如图（2），在菱形ABCD中，点E、F分别在BC、CD上，当∠BAD=120°，∠EAF=60°时，还有EF=BE+DF吗？
（2）在四边形ABCD中，点E、F分别在BC、CD上，当AB=AD，∠B+∠D=180，∠EAF=∠BAD时，EF=BE+DF吗？
归纳概括：反思前面的解答，思考每个条件的作用，可以得到一个结论“EF=BE+DF”的一般命题： 在四边形ABCD中，点E、F分别在BC、CD上，当AB=AD，∠B+∠D=180，∠EAF=∠BAD时，则EF=BE+DF ．
查看答案和解析>>
科目：初中数学 来源：2014年初中毕业升学考试（四川达州卷）数学（解析版） 题型：选择题
如图，在四边形ABCD中，∠A+∠D=α，∠ABC的平分线与∠BCD的平分线交于点P，则∠P=（ ）
A．90°﹣
α B．90°+α C．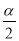
D．360°﹣α
查看答案和解析>>
科目：初中数学 来源：2014年初中毕业升学考试（四川资阳卷）数学（解析版） 题型：填空题
已知⊙O1与⊙O2的圆心距为6，两圆的半径分别是方程x2﹣5x+5=0的两个根，则⊙O1与⊙O2的位置关系是 ．
查看答案和解析>>
科目：初中数学 来源：2014年初中毕业升学考试（四川甘孜卷）数学（解析版） 题型：解答题
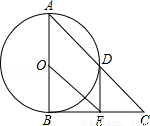
如图，在△ABC中，∠ABC=90°，以AB的中点O为圆心，OA为半径的圆交AC于点D，E是BC的中点，连接DE，OE．
（1）判断DE与⊙O的位置关系，并说明理由；
（2）求证：BC2=2CD•OE；
（3）若cos∠BAD=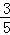
，BE=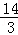
，求OE的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
