
�����о���ѧϰ��ʽ�������̲��о���ϰ���о�����ѧ�������⺣�����ѧϰ�����ʹ�����������Ч;����������һ��������ͬѧ�������Ķ����о�����ɡ���Ȳ��롱����������⣮
ϰ����
ϰ�� ��ͼ��1������E��F�ֱ���������ABCD�ı�BC��CD�ϣ���EAF=45�㣬����EF����EF=BE+DF��˵�����ɣ�
�����������ABCD�У�AB=AD����BAD=��ADC=��B=90�㣬
������ABE�Ƶ�A��ʱ����ת90������ADE�䣬��F��D��E����һ��ֱ���ϣ�
���E��AF=90�㩁45��=45��=��EAF��
����AE��=AE��AF=AF
���AE��F�ա�AEF��SAS��
��EF=E��F=DE��+DF=BE+DF��
ϰ���о�
�۲�������۲�ͼ��1�����ɽ���֪���������õ���������ABCD���ı��Σ���E��F�ֱ��ڱ�BC��CD�ϣ���AB=AD���ۡ�B=��D=90�㣻�ܡ�EAF= ��BAD��
��BAD��
��Ȳ��룺��1�����ı���ABCD�У���E��F�ֱ���BC��CD�ϣ���AB=AD����B=��Dʱ������EF=BE+DF��
�о�һ�����⣬�����������֣���ͬѧ���о�����ͼ��2����������ABCD�У���E��F�ֱ���BC��CD�ϣ�����BAD=120�㣬��EAF=60��ʱ������EF=BE+DF��
��2�����ı���ABCD�У���E��F�ֱ���BC��CD�ϣ���AB=AD����B+��D=180����EAF= ��BADʱ��EF=BE+DF��
��BADʱ��EF=BE+DF��
���ɸ�������˼ǰ��Ľ��˼��ÿ�����������ã����Եõ�һ�����ۡ�EF=BE+DF����һ�����⣺�����ı���ABCD�У���E��F�ֱ���BC��CD�ϣ���AB=AD����B+��D=180����EAF=��BADʱ����EF=BE+DF����

��1������BAD=120�㣬��EAF=60��ʱ��EF=BE+DF��������EF��BE+DF�����ɼ�������
��2����AB=AD����B+��D=180����EAF= ��BADʱ��EF=BE+DF���������ɼ�������
��BADʱ��EF=BE+DF���������ɼ�������
��������
�����������1���������ε����ʺ���EAF=60��õ�AB=AD����1+��3=60�㣬��B=��ADC=60�㣬�����ABE�Ƶ�A��ʱ����ת120������ADE�䣬��ͼ��2��������E��F��������ת�����ʵ���EAE��=120�㣬��1=��3��AE��=AE��DE��=BE����ADE��=��B=60�㣬����2+��3=60�㣬������EAF=��E��AF��Ȼ�����á�SAS��֤����AEF�աա�AE��F���õ�EF=E��F��������ADE��+��ADC=120�㣬���F��D��E�䲻���ߣ�����DE��+DF��EF������BE+DF��EF��
��2����ͼ��3��������AB=AD�������ABE�Ƶ�A��ʱ����ת��BAD�Ķ�������ADE�䣬������ת�����ʵ���EAE��=��BAD����1=��3��AE��=AE��DE��=BE����ADE��=��B��������B+��D=180������ADE��+��D =180�㣬���Ե�F��D��E�乲�ߣ�������EAF=��BAD���õ���1+��2=��BAD������2+��3=��BAD��������EAF=��E��AF��Ȼ�����á�SAS��֤����AEF�ա�AE��F���õ�EF=E��F������EF=DE��+DF= BE+DF������ǰ��������ͽ��ۿɹ���Ϊ�����ı���ABCD�У���E��F�ֱ���BC��CD�ϣ�������AB=AD����B+��D=180����EAF=��BADʱ������EF=BE+DF��
�����������1������BAD=120�㣬��EAF=60��ʱ��EF=BE+DF��������EF��BE+DF���������£�
��������ABCD�У���BAD=120�㣬��EAF=60�㣬
��AB=AD����1+��3=60�㣬��B=��ADC=60�㣬
������ABE�Ƶ�A��ʱ����ת120������ADE�䣬��ͼ��2��������E��F��

���EAE��=120�㣬��1=��3��AE��=AE��DE��=BE����ADE��=��B=60�㣬
���2+��3=60�㣬
���EAF=��E��AF��
����AEF����AE��F��
 ��
��
���AEF�ա�AE��F��SAS����
��EF=E��F��
�ߡ�ADE��+��ADC=120�㣬����F��D��E�䲻���ߣ�
��DE��+DF��EF
��BE+DF��EF��
��2����AB=AD����B+��D=180����EAF= ��BADʱ��EF=BE+DF������
��BADʱ��EF=BE+DF������
�������£���ͼ��3����

��AB=AD��
������ABE�Ƶ�A��ʱ����ת��BAD�Ķ�������ADE�䣬��ͼ��3����
���EAE��=��BAD����1=��3��AE��=AE��DE��=BE����ADE��=��B��
�ߡ�B+��D=180��
���ADE��+��D=180�㣬
����F��D��E�乲�ߣ�
�ߡ�EAF= ��BAD��
��BAD��
���1+��2= ��BAD��
��BAD��
���2+��3= ��BAD��
��BAD��
���EAF=��E��AF��
����AEF����AE��F��
 ��
��
���AEF�ա�AE��F��SAS����
��EF=E��F��
��EF=DE��+DF=BE+DF��
���ɣ����ı���ABCD�У���E��F�ֱ���BC��CD�ϣ���AB=AD����B+��D=180����EAF= ��BADʱ����EF=BE+DF��
��BADʱ����EF=BE+DF��
���㣺�ı����ۺ�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ�ɽ������������ѧ�������棩 ���ͣ������
��ͼ�������� ��x�ύ��A��5,0����B��-1,0�����㣬����A��ֱ��AC��x�ᣬ��ֱ��
��x�ύ��A��5,0����B��-1,0�����㣬����A��ֱ��AC��x�ᣬ��ֱ�� �ڵ�C��
�ڵ�C��
��1����������ߵĽ���ʽ��
��2�����A����ֱ�� �ĶԳƵ�
�ĶԳƵ�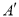 ���������ж���
���������ж��� �Ƿ����������ϣ���˵��������
�Ƿ����������ϣ���˵��������
��3����P����������һ���㣬����P��y���ƽ���ߣ����߶� �ڵ�M���Ƿ���������ĵ�P��ʹ�ı���PACM��ƽ���ı��Σ������ڣ������P�����ꣻ�������ڣ���˵������.
�ڵ�M���Ƿ���������ĵ�P��ʹ�ı���PACM��ƽ���ı��Σ������ڣ������P�����ꣻ�������ڣ���˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ����վ�����ѧ�������棩 ���ͣ�ѡ����
�����ĸ�����ʽ�У�����ʽ�ֽ���ǣ� ��
A��a2+1 B��a2��6a+9 C��x2+5y D��x2��5y
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��Ĵ��Ű�������ѧ�������棩 ���ͣ�ѡ����
��ƽ���ı���ABCD�У���E��AD�ϣ���AE��ED=3��1��CE���ӳ�����BA���ӳ��߽��ڵ�F����S��AFE��S�ı���ABCEΪ��������

A��3��4 B��4��3 C��7��9 D��9��7
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��Ĵ��Ű�������ѧ�������棩 ���ͣ�ѡ����
����0��1��1��x��3��4��ƽ������2�����������ݵ���λ���ǣ�������
A��1 B��3 C��1.5 D��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��Ĵ����ݾ�����ѧ�������棩 ���ͣ������
���ű�����ȫ��ͬ��ֽ�ƣ���ͼ��������������������ʾ��������ֱ�д���ĸ���ͬ��������С������4��ֽ�Ʊ��泯��ϴ�Ⱥ���������һ�ţ����Żأ�����������һ�ţ�

��1��д���������Ƴ��ֵ����п��ܵĽ����������������������ʾ����
��2�������������������ϵĽ��Ϊ�����������ж��ı���ABCDΪƽ���ı��εĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��Ĵ����ݾ�����ѧ�������棩 ���ͣ������
��ÿ�����һСʱ����������һ���ӡ����Կ�չ�����������˶���������ѧУʦ���Ķ�����ʶ����ǿ�ˣ�ijУ��ѧ��8200�ˣ�Ϊ�˽�ѧ��ÿ��Ķ���ʱ�䣬ѧУ��������������˲���ѧ����ͳ�ƽ�������
ʱ��� | Ƶ�� | Ƶ�� |
29���Ӽ����� | 108 | 0.54 |
30��39���� | 24 | 0.12 |
40��49���� | m | 0.15 |
50��59���� | 18 | 0.09 |
1Сʱ������ | 20 | 0.1 |
�����У�m=�� �����������ݵ��������� ������Уÿ�����ʱ��ﵽ1Сʱ��Լ���� ���ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��Ĵ�����������ѧ�������棩 ���ͣ������
��ͼ�����е�С������һ��־�Խ������ײ�ΪA��ij���ڰ��ߵ�B�����A��B�ı�ƫ��30��ķ����ϣ�Ȼ���ذ���ֱ��4���ﵽ��C�����ٴβ��A��C�ı�ƫ��45��ķ����ϣ�����A��B��C��ͬһƽ���ϣ����������־�Խ�����ײ�A������BC����̾��룮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��Ĵ�üɽ������ѧ�������棩 ���ͣ�ѡ����
���� ���Ա���x��ȡֵ��Χ���� ��
���Ա���x��ȡֵ��Χ���� ��
A�� B��
B�� C��
C�� D��
D��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com