在平行四边形ABCD中，点E在AD上，且AE：ED=3：1，CE的延长线与BA的延长线交于点F，则S△AFE：S四边形ABCE为（ ）
A．3：4 B．4：3 C．7：9 D．9：7
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源：2014年初中毕业升学考试（山东滨州卷）数学（解析版） 题型：选择题
王芳同学到文具店购买中性笔和笔记本.中性笔每支0.8元，笔记本每本1.2元，王芳带了10元钱，则可供她选择的购买方案的个数为（ ）（两样都买，余下的钱少于0.8元）
A．6 B．7 C．8 D． 9
查看答案和解析>>
科目：初中数学 来源：2014年初中毕业升学考试（安徽卷）数学（解析版） 题型：解答题
观察下列关于自然数的等式：
32-4×12=5 ①
52-4×22=9 ②
72-4×32=13 ③
…
根据上述规律解决下列问题：
（1）完成第四个等式：92—4×（ ）2=（ ）；
（2）写出你猜想的第n个等式（用含n的式子表示），并验证其正确性.
查看答案和解析>>
科目：初中数学 来源：2014年初中毕业升学考试（四川雅安卷）数学（解析版） 题型：解答题
如图，⊙O的直径CD垂直于弦AB，垂足为E，F为DC延长线上一点，且∠CBF=∠CDB．
（1）求证：FB为⊙O的切线；
（2）若AB=8，CE=2，求sin∠F．
查看答案和解析>>
科目：初中数学 来源：2014年初中毕业升学考试（四川雅安卷）数学（解析版） 题型：填空题
在平面直角坐标系中，O为坐标原点，则直线y=x+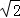
与以O点为圆心，1为半径的圆的位置关系为 ．
查看答案和解析>>
科目：初中数学 来源：2014年初中毕业升学考试（四川达州卷）数学（解析版） 题型：解答题
倡导研究性学习方式，着力教材研究，习题研究，是学生跳出题海，提高学习能力和创新能力的有效途径．下面是一案例，请同学们认真阅读、研究，完成“类比猜想”及后面的问题．
习题解答：
习题 如图（1），点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，则EF=BE+DF，说明理由．
解答：∵正方形ABCD中，AB=AD，∠BAD=∠ADC=∠B=90°，
∴把△ABE绕点A逆时针旋转90°至△ADE′，点F、D、E′在一条直线上．
∴∠E′AF=90°﹣45°=45°=∠EAF，
又∵AE′=AE，AF=AF
∴△AE′F≌△AEF（SAS）
∴EF=E′F=DE′+DF=BE+DF．
习题研究
观察分析：观察图（1），由解答可知，该题有用的条件是①ABCD是四边形，点E、F分别在边BC、CD上；②AB=AD；③∠B=∠D=90°；④∠EAF=
∠BAD．
类比猜想：（1）在四边形ABCD中，点E、F分别在BC、CD上，当AB=AD，∠B=∠D时，还有EF=BE+DF吗？
研究一个问题，常从特例入手，请同学们研究：如图（2），在菱形ABCD中，点E、F分别在BC、CD上，当∠BAD=120°，∠EAF=60°时，还有EF=BE+DF吗？
（2）在四边形ABCD中，点E、F分别在BC、CD上，当AB=AD，∠B+∠D=180，∠EAF=∠BAD时，EF=BE+DF吗？
归纳概括：反思前面的解答，思考每个条件的作用，可以得到一个结论“EF=BE+DF”的一般命题： 在四边形ABCD中，点E、F分别在BC、CD上，当AB=AD，∠B+∠D=180，∠EAF=∠BAD时，则EF=BE+DF ．
查看答案和解析>>
科目：初中数学 来源：2014年初中毕业升学考试（四川达州卷）数学（解析版） 题型：选择题
如图，在四边形ABCD中，∠A+∠D=α，∠ABC的平分线与∠BCD的平分线交于点P，则∠P=（ ）
A．90°﹣
α B．90°+α C．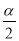
D．360°﹣α
查看答案和解析>>
科目：初中数学 来源：2014年初中毕业升学考试（四川眉山卷）数学（解析版） 题型：填空题
如图，在?ABCD中，AB=3，BC=5，对角线AC、BD相交于点O，过点O作OE⊥AC，交AD于点E，连接CE，则△CDE的周长为__________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
