
“每天锻炼一小时,健康生活一辈子”,自开展“阳光体育运动”以来,学校师生的锻炼意识都增强了,某校有学生8200人,为了解学生每天的锻炼时间,学校体育组随机调查了部分学生,统计结果如表.
时间段 | 频数 | 频率 |
29分钟及以下 | 108 | 0.54 |
30﹣39分钟 | 24 | 0.12 |
40﹣49分钟 | m | 0.15 |
50﹣59分钟 | 18 | 0.09 |
1小时及以上 | 20 | 0.1 |
表格中,m= ;这组数据的众数是 ;该校每天锻炼时间达到1小时的约有 人.
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案科目:初中数学 来源:2014年初中毕业升学考试(山东济宁卷)数学(解析版) 题型:选择题
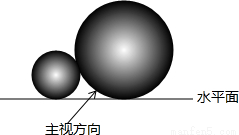
如图,两个直径分别为36cm和16cm的球,靠在一起放在同一水平面上,组成如图所示的几何体,则该几何体的俯视图的圆心距是[来( )源:Zxxk.Com]
A.10cm. B.24cm C.26cm. D.52cm.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川雅安卷)数学(解析版) 题型:填空题
在平面直角坐标系中,O为坐标原点,则直线y=x+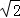 与以O点为圆心,1为半径的圆的位置关系为 .
与以O点为圆心,1为半径的圆的位置关系为 .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川达州卷)数学(解析版) 题型:解答题
倡导研究性学习方式,着力教材研究,习题研究,是学生跳出题海,提高学习能力和创新能力的有效途径.下面是一案例,请同学们认真阅读、研究,完成“类比猜想”及后面的问题.
习题解答:
习题 如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,说明理由.
解答:∵正方形ABCD中,AB=AD,∠BAD=∠ADC=∠B=90°,
∴把△ABE绕点A逆时针旋转90°至△ADE′,点F、D、E′在一条直线上.
∴∠E′AF=90°﹣45°=45°=∠EAF,
又∵AE′=AE,AF=AF
∴△AE′F≌△AEF(SAS)
∴EF=E′F=DE′+DF=BE+DF.
习题研究
观察分析:观察图(1),由解答可知,该题有用的条件是①ABCD是四边形,点E、F分别在边BC、CD上;②AB=AD;③∠B=∠D=90°;④∠EAF= ∠BAD.
∠BAD.
类比猜想:(1)在四边形ABCD中,点E、F分别在BC、CD上,当AB=AD,∠B=∠D时,还有EF=BE+DF吗?
研究一个问题,常从特例入手,请同学们研究:如图(2),在菱形ABCD中,点E、F分别在BC、CD上,当∠BAD=120°,∠EAF=60°时,还有EF=BE+DF吗?
(2)在四边形ABCD中,点E、F分别在BC、CD上,当AB=AD,∠B+∠D=180,∠EAF= ∠BAD时,EF=BE+DF吗?
∠BAD时,EF=BE+DF吗?
归纳概括:反思前面的解答,思考每个条件的作用,可以得到一个结论“EF=BE+DF”的一般命题: 在四边形ABCD中,点E、F分别在BC、CD上,当AB=AD,∠B+∠D=180,∠EAF=∠BAD时,则EF=BE+DF .

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川达州卷)数学(解析版) 题型:选择题
如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠P=( )

A.90°﹣ α B.90°+
α B.90°+ α C.
α C.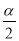 D.360°﹣α
D.360°﹣α
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川资阳卷)数学(解析版) 题型:解答题
如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),其顶点为C,对称轴为x=1.
(1)求抛物线的解析式;
(2)已知点M为y轴上的一个动点,当△ABM为等腰三角形时,求点M的坐标;
(3)将△AOB沿x轴向右平移m个单位长度(0<m<3)得到另一个三角形,将所得的三角形与△ABC重叠部分的面积记为S,用m的代数式表示S.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川资阳卷)数学(解析版) 题型:选择题
如图,在Rt△ABC中,∠BAC=90°.如果将该三角形绕点A按顺时针方向旋转到△AB1C1的位置,点B1恰好落在边BC的中点处.那么旋转的角度等于( )

A.55° B.60° C.65° D.80°
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川甘孜卷)数学(解析版) 题型:解答题
如图,在?ABCD中,E,F分别为BC,AB中点,连接FC,AE,且AE与FC交于点G,AE的延长线与DC的延长线交于点N.
(1)求证:△ABE≌△NCE;
(2)若AB=3n,FB= GE,试用含n的式子表示线段AN的长.
GE,试用含n的式子表示线段AN的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com