
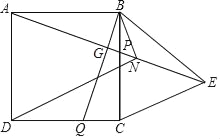
【题目】如图,在正方形ABCD中,点P、Q分别为BC、CD边上一点,且BP=CQ=![]() BC,连接AP、BQ交于点G,在AP的延长线上取一点E,使GE=AG,连接BE、CE.∠CBE的平分线BN交AE于点N,连接DN,若DN=
BC,连接AP、BQ交于点G,在AP的延长线上取一点E,使GE=AG,连接BE、CE.∠CBE的平分线BN交AE于点N,连接DN,若DN=![]() ,则CE的长为_____.
,则CE的长为_____.
【答案】![]()
【解析】分析:首先得出∠AGB=90°,过点D作DM⊥AN于M,根据五点共圆的性质得出Rt△DMN,Rt△BGN都是等腰直角三角形,然后根据DN的长度得出正方形的边长,根据△ABP的等积法得出BG的长度,然后根据△BGP和△CNP相似得出CN的长度,最后根据等腰直角三角形的性质得出CE的长度.
详解:∵BP=CQ,则△ABP≌△BCQ,∴∠AGB=90°,
连接CN,延长BN交CE于H. 过点D作DM⊥AN于M,
∴Rt△ADM≌Rt△ABG,DM=AG, ∵BN平分∠CBE,∴CH=HE,
∵∠CBN=∠EBN,BE=BC,BN=BN, ∴△BCN≌△BEN,
∴CN=NE,△CEN是等腰三角形,
延长AE交DC延长线于F,则有:∠BAG=∠BEG=∠CFE=∠BCN,
A,B,C,D,N五点共圆,∠AND=∠BNG=45°[AB弦所对圆周角=45°]
Rt△DMN,Rt△BGN都是等腰直角三角形,
∵DN=![]() , ∴AB=MN=
, ∴AB=MN=![]() ,根据△ABP的等积法可得:BG=
,根据△ABP的等积法可得:BG=![]() ,
,
∵△BGP∽△CNP,则CN=2BG=![]() ,则CE=
,则CE=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣
x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣![]() x2+bx+c经过点A,B.
x2+bx+c经过点A,B.
(1)求点B的坐标和抛物线的解析式;
(2)M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.
①点M在线段OA上运动,若以B,P,N为顶点的三角形与△APM相似,求点M的坐标;
②点M在x轴上自由运动,若三个点M,P,N中恰有一点是其它两点所连线段的中点(三点重合除外),则称M,P,N三点为“共谐点”.请直接写出使得M,P,N三点成为“共谐点”的m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
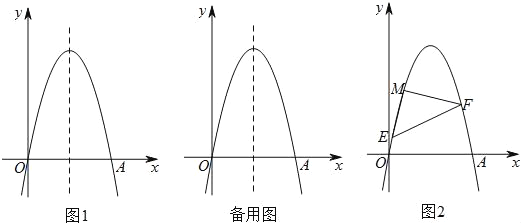
【题目】如图1,抛物线y=﹣x2+6x与x轴交于O、A两点,点P在抛物线上,过点P的直线y=x+m与抛物线的对称轴交于点Q.
(1)这条抛物线的对称轴是:直线 ,直线PQ与x轴所夹锐角的度数是 度;
(2)若S△POQ:S△PAQ=1:2,求此时的点P坐标;
(3)如图2,点M(1,5)在抛物线上,以点M为直角顶点作Rt△MEF,且E、F均在抛物线上,则所有满足条件的直线EF必然经过定点N,求点N坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小李做摸球试验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是试验中的一组统计数据:
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数m | 63 | 124 | 178 | 302 | 488 | 600 | 1800 |
摸到白球的频率 | 0.63 | 0.62 | 0.593 | 0.604 | 0.61 |
|
|
(1)完成上表;
(2)若从盒子中随机摸出一个球,则摸到白球的概率P= ;(结果保留小数点后一位)
(3)估算这个不透明的盒子里白球有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣2,﹣1,0,1,2,3这六个数中,任取一个数作为a的值,恰好使得关于x、y的二元一次方程组![]() 有整数解,且方程ax2+ax+1=0有实数根的概率是_____.
有整数解,且方程ax2+ax+1=0有实数根的概率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
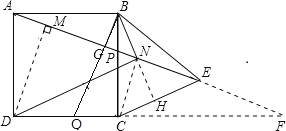
【题目】如图1,已知在平面直角坐标系中,A(![]() ,0),B(4,0),C(0,3),过点C作CD∥x轴,与直线AD交于点D,直线AD与y轴交于点E,连接AC、BD,且tan∠DAB=
,0),B(4,0),C(0,3),过点C作CD∥x轴,与直线AD交于点D,直线AD与y轴交于点E,连接AC、BD,且tan∠DAB=![]() .
.

(1)求直线AD的解析式和线段BD所在直线的解析式.
(2)如图2,将△CAD沿着直线CD向右平移得△C1A1D1,当C1A1⊥EA1时,在x轴上是否存在点M,使△A1D1M是以A1D1为腰的等腰三角形,若存在,求出△A1D1M的周长;若不存在,请说明理由.
(3)如图3,延长DB至F,使得BF=DB,点K为线段AD上一动点,连接KF、BK,将△FBK沿BK翻折得△F′BK,请直接写出当DK为何值时,△F′BK与△DBK的重叠部分的面积恰好是△FKD的面积的![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 于点
于点![]() ,点
,点![]() 为
为![]() 边的中点,过点
边的中点,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.
![]() 如图
如图![]() ,求证:四边形
,求证:四边形![]() 是矩形;
是矩形;
![]() 如图
如图![]() ,当
,当![]() 时,取
时,取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,在不添加任何辅助线和字母的条件下,请直接写出图中所有的平行四边形(不包括矩形
,在不添加任何辅助线和字母的条件下,请直接写出图中所有的平行四边形(不包括矩形![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“2016年联欢会”中,有一个摸奖游戏:有4张纸牌,背面都是喜羊羊头像,正面有2张是笑脸,2张是哭脸,现将4张纸牌洗匀后背面朝上摆放到桌上,然后让同学去翻纸牌.
(1)现在小芳和小霞分别有一次翻牌机会,若正面是笑脸,则小芳获奖;若正面是哭脸,则小霞获奖,她们获奖的机会相同吗?判断并说明理由.
(2)如果小芳、小明都有翻两张牌的机会.翻牌规则:小芳先翻一张,放回后再翻一张;小明同时翻开两张纸牌.他们翻开的两张纸牌中只要出现笑脸就获奖.请问他们获奖的机会相等吗?判断并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com