
 如图,在△ABC中,AB=BC,∠ABC=100°,边BA绕点B顺时针旋转m°,(0<m<180)得到线段BD,连接AD、DC,若△ADC为等腰三角形,则m所有可能的取值是130或100或160.
如图,在△ABC中,AB=BC,∠ABC=100°,边BA绕点B顺时针旋转m°,(0<m<180)得到线段BD,连接AD、DC,若△ADC为等腰三角形,则m所有可能的取值是130或100或160. 分析 由旋转的性质得出BD=AB=BC,分三种情况:①当DA=DC时;②当AD=AC时;③当CA=CD时;分别求出m的值即可.
解答 解:由旋转的性质得:BD=AB=BC,
∵△ADC为等腰三角形,
∴分三种情况:
①当DA=DC时,∠ABD=∠CBD=$\frac{1}{2}$(360°-∠ABC)=130°,
∴m=130;
②当AD=AC时,∠ABD=∠ABC=100°,
∴m=100;
③当CA=CD时,∠CBD=∠ABC=100°,
∴∠ABD=360°-100°-100°=160°,
∴m=160;
综上所述:m所有可能的取值为130或100或160;
故答案为:130或100或160.
点评 本题考查了旋转的性质、等腰三角形的性质;熟练掌握旋转的性质和等腰三角形的性质,进行分类讨论是解决问题的关键.


 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC是等边三角形,D、E、F分别是射线BA、CB、AC上一点,且AD=BE=CF,连接DE、EF、DF.
如图,已知△ABC是等边三角形,D、E、F分别是射线BA、CB、AC上一点,且AD=BE=CF,连接DE、EF、DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
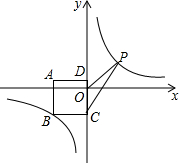 如图,正方形ABCD在平面直角坐标系中,且AD∥x轴,点A的坐标为(-4,1),点D的坐标为(0,1),点B,P都在反比例函数y=$\frac{k}{x}$的图象上,且P时动点,连接OP,CP.
如图,正方形ABCD在平面直角坐标系中,且AD∥x轴,点A的坐标为(-4,1),点D的坐标为(0,1),点B,P都在反比例函数y=$\frac{k}{x}$的图象上,且P时动点,连接OP,CP.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com