
【题目】如图1,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、点
、点![]() ,与
,与![]() 轴交于点
轴交于点![]() ;直线
;直线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是第一象限内抛物线上一动点.
是第一象限内抛物线上一动点.
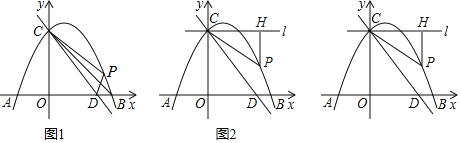
(1)求抛物线的解析式;
(2)若![]() ,求
,求![]() 的面积;
的面积;
(3)如图2,过点![]() 作直线
作直线![]() 轴,过点
轴,过点![]() 作
作![]() 于点
于点![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转,使点
顺时针旋转,使点![]() 的对应点
的对应点![]() 恰好落在直线
恰好落在直线![]() 上,同时使点
上,同时使点![]() 的对应点
的对应点![]() 恰好落在坐标轴上,请直接写出此时点
恰好落在坐标轴上,请直接写出此时点![]() 的坐标.
的坐标.
【答案】(1) y=-![]() x2+x+4 (2)
x2+x+4 (2) ![]() (3) 点P坐标为(
(3) 点P坐标为(![]() )或(
)或(![]() )
)
【解析】
(1)由于抛物线交y轴于点C,直线y=-![]() x+4也经过点C,令x=0代入直线即求得点C坐标.再用待定系数法即求出抛物线解析式.
x+4也经过点C,令x=0代入直线即求得点C坐标.再用待定系数法即求出抛物线解析式.
(2)由OB=OC可得∠OBC=45°,所以过点D作BC的垂线并交直线CP于点F,可证得∠OBF=45°,即得到点F横坐标与B相等,纵坐标=BF=BD,由直线CD解析式求得点D即求出BD的长,进而得点F坐标,可求直线CP解析式.把直线CP解析式与抛物线解析式联立方程组即求得点P坐标.求直线CP与x轴交点G,可得△PCD面积等于△CDG面积减去△PDG面积,代入计算即求得△PCD面积.
(3)由于点P'落在坐标轴上,故有两种情况需分类讨论.①当点P'在y轴上时,由∠PCH=∠P'CH'与∠OCB=∠BCH=45°可得∠DCB=∠PCB,由第(2)可知此时P(![]() ,
,![]() ).②当点P'在x轴上时,设点P横坐标为p,则能用p表示P'H'、CH'.过点H'作x轴的垂线MN,证得∠H'P'M=∠CH'N=∠OCD,则由∠OCD的三角函数值可求得用p表示的MH'即列方程,进而求得p的值.
).②当点P'在x轴上时,设点P横坐标为p,则能用p表示P'H'、CH'.过点H'作x轴的垂线MN,证得∠H'P'M=∠CH'N=∠OCD,则由∠OCD的三角函数值可求得用p表示的MH'即列方程,进而求得p的值.
(1)∵当x=0时,y=-![]() x+4=4
x+4=4
∴C(0,4)
∵抛物线y=-![]() x2+bx+c过点B(4,0)、C(0,4)
x2+bx+c过点B(4,0)、C(0,4)
∴![]() 解得:
解得:![]()
∴抛物线解析式为y=-![]() x2+x+4
x2+x+4
(2)如图1,直线CP与x轴交于点G,过点D作DE⊥CB于点E,交直线CP于点F,连接BF.
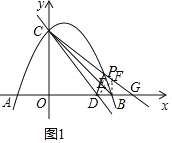
∴∠CED=∠CEF=90°
在△CDE与△CFE中
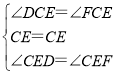
∴△CDE≌△CFE(ASA)
∴DE=FE,即BC垂直平分DF
∴BD=BF
∵B(4,0),C(0,4)
∴∠OBC=45°
∴∠CBF=∠OBC=45°
∴∠DBF=90°
∵当y=-![]() x+4=0时,解得:x=3
x+4=0时,解得:x=3
∴D(3,0)
∴BF=BD=4-3=1
∴F(4,1)
设直线CF解析式为y=kx+4
∴4k+4=1 解得:k=-![]()
∴直线CP:y=-![]() x+4
x+4
当y=0时,-![]() x+4=0,解得:x=
x+4=0,解得:x=![]()
∴G(![]() ,0),DG=
,0),DG=![]() -3=
-3=![]()
∵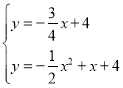
解得: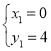 (即点C),
(即点C),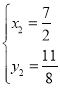
∴P(![]() )
)
∴S△PCD=S△CDG-S△PDG=![]() DGOC-
DGOC-![]() DGyP=
DGyP=![]() DG(OC-yP)=
DG(OC-yP)=![]() ×
×![]() ×(4-
×(4-![]() )=
)=![]()
∴△PCD的面积为![]()
(3)①若点P'落在y轴上,如图2,
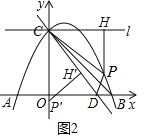
∵△CPH绕点C旋转得△CP'H',H'在直线CD上
∴∠PCH=∠PCH'
∵∠OCB=∠BCH=45°
∴∠OCB-∠OCH'=∠BCH-∠PCH
即∠DCB=∠PCB
由(2)可得此时点P(![]() )
)
②若点P'落在x轴上,如图3,过点H'作MN⊥x轴于点M,交直线l于点N
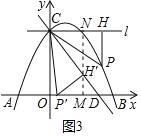
∴四边形OCNM是矩形
∴MN=OC=4,
∵OD=3,∠COD=90°
∴CD=![]()
∴sin∠OCD=![]() ,cos∠OCD=
,cos∠OCD=![]() ,
,
设点P坐标(p,-![]() p2+p+4)(0<p<4)
p2+p+4)(0<p<4)
∴CH'=CH=p,P'H'=PH=4-(-![]() p2+p+4)=
p2+p+4)=![]() p2-p
p2-p
∵MN∥y轴
∴∠CH'N=∠OCD
∴Rt△CNH'中,cos∠CH'N= ![]()
∴NH'=![]() CH'=
CH'=![]() p
p
∴MH'=MN-NH'=4-![]() p
p
∵∠P'MH'=∠P'H'C=90°
∴∠P'H'M+∠CH'N=∠P'H'M+∠H'P'M=90°
∴∠H'P'M=∠CH'N
∴Rt△H'P'M中,sin∠H'P'M=![]()
∴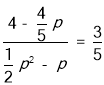
解得:p1=-4(舍去),p2=![]()
∴-![]() p2+p+4=-
p2+p+4=-![]()
∴P(![]() )
)
综上所述,点P坐标为(![]() )或(
)或(![]() )
)


科目:初中数学 来源: 题型:
【题目】某学校去年在某商场购买甲、乙两种不同足球,购买甲种足球共花费2400元,购买乙种足球共花费1600元,购买甲种足球数量是购买乙种足球数量的2倍.且购买一个乙种足球比购买一个甲种足球多花20元.
(1)求购买一个甲种足球、一个乙种足球各需多少元;
(2)今年学校为编排“足球操”,决定再次购买甲、乙两种足球共50个.如果两种足球的单价没有改变,而此次购买甲、乙两种足球的总费用不超过3500元,那么这所学校最少可购买多少个甲种足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E为长方形纸片ABCD的边CD上一点,将纸片沿AE对折,点D的对应点D′恰好在线段BE上.若AD=3,DE=1,则AB=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线l过点(0,2),且与x轴平行;直线![]() 与y轴交于A点,与直线l交于B点;抛物线
与y轴交于A点,与直线l交于B点;抛物线![]() 的顶点为C.
的顶点为C.
(1)求A,B两点的坐标;
(2)求点C的坐标(用m表示);
(3)若抛物线![]() 与线段AB有公共点,求m的取值范围.
与线段AB有公共点,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近日,深圳市人民政府发布了《深圳市可持续发展规划》,提出了要做可持续发展的全球创新城市的目标,某初中学校了解学生的创新意识,组织了全校学生参加创新能力大赛,从中抽取了部分学生成绩,分为5组:A组50~60;B组60~70;C组70~80;D组80~90;E组90~100,统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图.
(1)抽取学生的总人数是 人,扇形C的圆心角是 °;
(2)补全频数直方图;
(3)该校共有2200名学生,若成绩在70分以下(不含70分)的学生创新意识不强,有待进一步培养,则该校创新意识不强的学生约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形![]() 中,点
中,点![]() 是对角线
是对角线![]() 上的动点(与点
上的动点(与点![]() 不重合),连接
不重合),连接![]() .
.
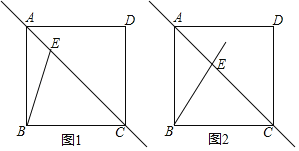
(1)将射线![]() 绕点
绕点![]() 顺时针旋转45°,交直线
顺时针旋转45°,交直线![]() 于点
于点![]() .
.
①依题意补全图1;
②小研通过观察、实验,发现线段![]() ,
,![]() ,
,![]() 存在以下数量关系:
存在以下数量关系:
![]() 与
与![]() 的平方和等于
的平方和等于![]() 的平方.小研把这个猜想与同学们进行交流,通过讨论,形成证明该猜想的几种想法:
的平方.小研把这个猜想与同学们进行交流,通过讨论,形成证明该猜想的几种想法:
想法1:将线段![]() 绕点
绕点![]() 逆时针旋转90°,得到线段
逆时针旋转90°,得到线段![]() ,要证
,要证![]() 的关系,只需证
的关系,只需证![]() 的关系.
的关系.
想法2:将![]() 沿
沿![]() 翻折,得到
翻折,得到![]() ,要证
,要证![]() 的关系,只需证
的关系,只需证![]() 的关系.
的关系.
…
请你参考上面的想法,用等式表示线段![]() 的数量关系并证明;(一种方法即可)
的数量关系并证明;(一种方法即可)
(2)如图2,若将直线![]() 绕点
绕点![]() 顺时针旋转135°,交直线
顺时针旋转135°,交直线![]() 于点
于点![]() .小研完成作图后,发现直线
.小研完成作图后,发现直线![]() 上存在三条线段(不添加辅助线)满足:其中两条线段的平方和等于第三条线段的平方,请直接用等式表示这三条线段的数量关系.
上存在三条线段(不添加辅助线)满足:其中两条线段的平方和等于第三条线段的平方,请直接用等式表示这三条线段的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=﹣2x2+4x+m+1,与x轴的公共点为A,B.
(1)如果A与B重合,求m的值;
(2)横、纵坐标都是整数的点叫做整点:
①当m=﹣1时,求线段AB上整点的个数;
②若设抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)整点的个数为n,当1<n≤8时,结合函数的图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+2ax﹣3a(a>0)与x轴交于A,B两点(点A在点B的左侧).
(1)求抛物线的对称轴及线段AB的长;
(2)抛物线的顶点为P,若∠APB=120°,求顶点P的坐标及a的值;
(3)若在抛物线上存在一点N,使得∠ANB=90°,结合图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系xOy中,直线y=mx与双曲线![]() 相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.
相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.
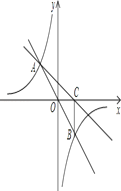
(1)求m、n的值;
(2)求直线AC的解析式.
(3)点P在双曲线上,且△POC的面积等于△ABC面积的![]() ,求点P的坐标。
,求点P的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com