
【题目】在平面直角坐标系中,已知![]() ,
,![]() .
.
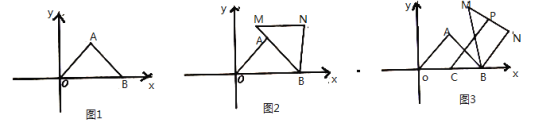
(1)如图1,求![]() 的值.
的值.
(2)把![]() 绕着点
绕着点![]() 顺时针旋转,点
顺时针旋转,点![]() 、
、![]() 旋转后对应的点分别为
旋转后对应的点分别为![]() 、
、![]() .
.
①当![]() 恰好落在
恰好落在![]() 的延长线上时,如图2,求出点
的延长线上时,如图2,求出点![]() 、
、![]() 的坐标.
的坐标.
②若点![]() 是
是![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 上的动点,如图3,在旋转过程中,请直接写出线段
上的动点,如图3,在旋转过程中,请直接写出线段![]() 长的取值范围.
长的取值范围.
【答案】(1)![]() ;(2)①
;(2)①![]() ,②
,②![]() ;(3)
;(3)![]()
【解析】
(1)作AH⊥OB,根据正弦的定义即可求解;
(2)作MC⊥OB,先求出直线AB解析式,根据等腰三角形的性质及三角函数的定义求出M点坐标,根据MN∥OB,求出N点坐标;
(3)由于点C是定点,点P随△ABO旋转时的运动轨迹是以B为圆心,BP长为半径的圆,故根据点和圆的位置关系可知,当点P在线段OB上时,CP=BP-BC最短;当点P在线段OB延长线上时,CP=BP+BC最长.又因为BP的长因点D运动而改变,可先求BP长度的范围.由垂线段最短可知,当BP垂直MN时,BP最短,求得的BP代入CP=BP-BC求CP的最小值;由于BM>BN,所以点P与M重合时,BP=BM最长,代入CP=BP+BC求CP的最大值.
(1)作AH⊥OB,
∵![]() ,
,![]() .
.
∴H(3,5)
∴AH=3,AH=![]()
∴![]() =
=![]() =
=![]()
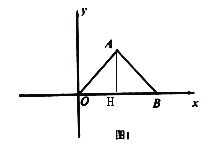
(2)由(1)得A(3,4),又![]()
求得直线AB的解析式为:y=![]()
∵旋转,∴MB=OB=6,
作MC⊥OB,∵AO=BO,
∴∠AOB=∠ABO
∴MC=MBsin∠ABO=6×![]() =
=![]()
即M点的纵坐标为![]() ,代入直线AB得x=
,代入直线AB得x=![]()
∴![]() ,
,
∵∠NMB=∠AOB=∠ABO
∴MN∥OB,又MN=AB=5,
则![]() +5=
+5=![]()
∴![]()
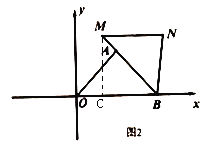
(3)连接BP
∵点D为线段OA上的动点,OA的对应边为MN
∴点P为线段MN上的动点
∴点P的运动轨迹是以B为圆心,BP长为半径的圆
∵C在OB上,且CB=![]() OB=3
OB=3
∴当点P在线段OB上时,CP=BPBC最短;当点P在线段OB延长线上时,CP=BP+BC最长
如图3,当BP⊥MN时,BP最短
∵S△NBM=S△ABO,MN=OA=5
∴![]() MNBP=
MNBP=![]() OByA
OByA
∴BP=![]() =
=![]() =
=![]()
∴CP最小值=![]() 3=
3=![]()
当点P与M重合时,BP最大,BP=BM=OB=6
∴CP最大值=6+3=9
∴线段CP长的取值范围为![]() .
.


科目:初中数学 来源: 题型:
【题目】请用学过的方法研究一类新函数![]() (
(![]() 为常数,
为常数,![]() )的图象和性质.
)的图象和性质.
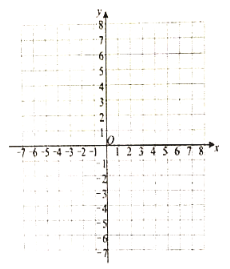
(1)在给出的平面直角坐标系中画出函数![]() 的图象;
的图象;
(2)对于函数![]() ,当自变量
,当自变量![]() 的值增大时,函数值
的值增大时,函数值![]() 怎样变化?
怎样变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2019大洋湾盐城马拉松”的赛事共有三项:A,“全程马拉松”、B,“半程马拉松”、C.“迷你健身跑”,小明和小刚参与了该项赛事的志愿者服务工作,组委会随机将志愿者分配到三个项目组.
(1)小明被分配到“迷你健身跑”项目组的概率为 ;
(2)求小明和小刚被分配到不同项目组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进A,B两种型号的手机,已知每部A型号手机的进价比每部B型号手机进价多500元,若商场用50000元共购进A型号手机10部,B型号手机20部,求A、B两种型号的手机每部进价各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
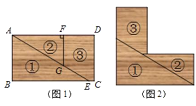
【题目】在综合实践课中,小慧将一张长方形卡纸如图1所示裁剪开,无缝隙不重叠的拼成如图2所示的“![]() ”形状,且成轴对称图形.裁剪过程中卡纸的消耗忽略不计,若已知
”形状,且成轴对称图形.裁剪过程中卡纸的消耗忽略不计,若已知![]() ,
,![]() ,
,![]() .
.
求(1)线段![]() 与
与![]() 的差值是___
的差值是___
(2)![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=5,AD=3,动点P满足S△PAB=![]() S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为_____.
S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组想测量一棵树的高度,在阳光下,一名同学测得一根长为1m的竹竿的影长为0.5m,同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上,其中,落在墙壁上的影长为0.8m,落在地面上的影长为4.4m,则树的高为_______m.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com