
【题目】一张圆形纸片,小芳进行了如下连续操作:
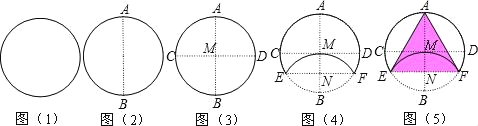
(1)将圆形纸片左右对折,折痕为AB,如图(2)所示.
(2)将圆形纸片上下折叠,使A、B两点重合,折痕CD与AB相交于M,如图(3)所示.
(3)将圆形纸片沿EF折叠,使B、M两点重合,折痕EF与AB相交于N,如图(4)所示.
(4)连结AE、AF,如图(5)所示.
经过以上操作小芳得到了以下结论:
①CD∥EF;②四边形MEBF是菱形;③△AEF为等边三角形;④![]() ,
,
以上结论正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】
试题根据折叠的性质,纸片上下折叠A、B两点重合,可得∠BMD=90°,纸片沿EF折叠,B、M两点重合,∠BNF=90°,所以∠BMD=∠BNF=90°,然后利用同位角相等,两直线平行可得CD∥EF,从而判定①正确;根据垂径定理可得BM垂直平分EF,又∵纸片沿EF折叠,B、M两点重合,BN=MN,从而得到BM、EF互相垂直平分,然后根据对角线互相垂直平分的四边形是菱形得出四边形MEBF是菱形,从而得到②正确;根据直角三角形30°角所对的直角边等于斜边的一半,即ME=MB=2MN,得出∠MEN=30°,然后求出∠EMN=90°﹣30°=60°,根据等边对等角,即AM=ME得出∠AEM=∠EAM,然后利用三角形的一个外角等于与它不相邻的两个内角的和求出∠AEM=![]() ∠EMN=
∠EMN=![]() ×60°=30°,从而得到∠AEF=60°,同理求∠AFE=60°,再根据三角形的内角和等于180°求出∠EAF=60°,从而判定△AEF是等边三角形,故③正确;设圆的半径为r,则EN=
×60°=30°,从而得到∠AEF=60°,同理求∠AFE=60°,再根据三角形的内角和等于180°求出∠EAF=60°,从而判定△AEF是等边三角形,故③正确;设圆的半径为r,则EN=![]() r,可得EF=2EN=
r,可得EF=2EN=![]() r,即可得S四边形AEBF:S扇形BEMF=(
r,即可得S四边形AEBF:S扇形BEMF=(![]() ×
×![]() r×2r):(
r×2r):(![]() πr2)=3
πr2)=3![]() :π,故④正确;综上所述,结论正确的是①②③④共4个.故选D.
:π,故④正确;综上所述,结论正确的是①②③④共4个.故选D.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】如图,把一张矩形纸片ABCD沿对角线BD折叠,使点C落
在E处,BE与AD相交于F,下列结论:①BD2=AD2+AB2
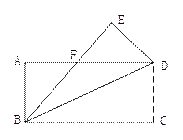 ②△ABF≌△EDF ③
②△ABF≌△EDF ③![]() ④AD=BD·cos45°正确的是( )
④AD=BD·cos45°正确的是( )
A. ①② B. ②③ C. ①④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某手机销售商从厂家购进了![]() 两种型号的手机,已知一台
两种型号的手机,已知一台![]() 型手机的进价比一台
型手机的进价比一台![]() 型手机的进价多300元,用7500元购进
型手机的进价多300元,用7500元购进![]() 型手机和用6000元购进
型手机和用6000元购进![]() 型手机的数量相同.
型手机的数量相同.
(1)求一台![]() 型手机和一台
型手机和一台![]() 型手机的进价各是多少元?
型手机的进价各是多少元?
(2)在销售过程中,![]() 型手机因为性价比高,更受消费者的欢迎.为了增大
型手机因为性价比高,更受消费者的欢迎.为了增大![]() 型手机的销量,该销售商决定对
型手机的销量,该销售商决定对![]() 型手机进行降价销售.经调查,当
型手机进行降价销售.经调查,当![]() 型手机的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台.如果每天销售
型手机的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台.如果每天销售![]() 型手机的利润为3200元,请问该手机销售商应将
型手机的利润为3200元,请问该手机销售商应将![]() 型手机的售价降低多少元?
型手机的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
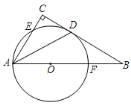
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC、AB于点E、F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=![]() ,BF=2,求⊙O的半径.
,BF=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象经过点A(﹣1,0)和点B(3,0),且有最小值为﹣2.
(1)求这个函数的解析式;
(2)函数的开口方向、对称轴;
(3)当y>0时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
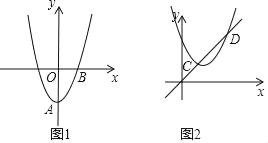
【题目】如图1,在平面直角坐标系中,抛物线C1:y=ax2+bx﹣a2关于y轴对称且有最小值﹣1.
(1)求抛物线C1的解析式;
(2)在图1中抛物线C1顶点为A,将抛物线C1绕 点B旋转180°后得到抛物线C2,直线y=kx﹣2k+4总经过一定点M,若过定点M的直线与抛物线C2只有一个公共点,求直线l的解析式.
(3)如图2,先将抛物线 C1向上平移使其顶点在原点O,再将其顶点沿直线y=x平移得到抛物线C3,设抛物线C3与直线y=x交于C、D两点,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
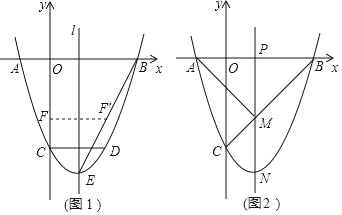
【题目】如图1,二次函数y=x2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,OB=OC.点D在函数图象上,CD∥x轴,且CD=4,直线1是抛物线的对称轴,E是抛物线的顶点.
(1)求b、c的值;
(2)如图1,连接BE,线段OC上的点F关于直线l的对称点F'恰好在线段BE上,求点F的坐标;
(3)如图2,动点P在线段OB上,过点P作x轴的垂线分别与BC交于点M,与抛物线交于点N.抛物线上有一点Q,使得△PQN与△APM的面积相等,请求出点Q到直线PN的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com