
����Ŀ����ͼ1�����κ���y��x2+bx+c��ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�C��OB��OC����D�ں���ͼ���ϣ�CD��x�ᣬ��CD��4��ֱ��1�������ߵĶԳ��ᣬE�������ߵĶ��㣮
��1����b��c��ֵ��
��2����ͼ1������BE���߶�OC�ϵĵ�F����ֱ��l�ĶԳƵ�F'ǡ�����߶�BE�ϣ����F�����ꣻ
��3����ͼ2������P���߶�OB�ϣ�����P��x��Ĵ��߷ֱ���BC���ڵ�M���������߽��ڵ�N������������һ��Q��ʹ�á�PQN���APM�������ȣ��������Q��ֱ��PN�ľ��룮
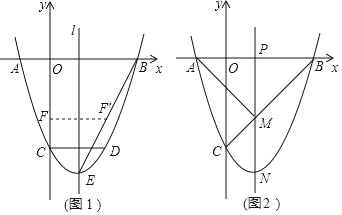
���𰸡���1��b����4��c����5����2����F������Ϊ��0����3������3����Q��ֱ��PN�ľ���Ϊ1��
��������
��1��CD��4�������Գ���x��2����![]() b������b����4����������ʽΪ��y��x2��4x+c��OB��OC�����B����Ϊ����c��0�����ѵ�B������뺯������ʽ��������⣻
b������b����4����������ʽΪ��y��x2��4x+c��OB��OC�����B����Ϊ����c��0�����ѵ�B������뺯������ʽ��������⣻
��2��ֱ��BE�ı���ʽΪ��y��3x��15����x��4������ʽ�ã�y��3��4��15����3������������ΪF�䣨4����3����������⣻
��3��S��APM��![]() ��PM��AP��S��PQN��
��PM��AP��S��PQN��![]() ��PN��d������S��PQN��S��APM��������⣮
��PN��d������S��PQN��S��APM��������⣮
��1��CD��4�������Գ���x��2����![]() b������b����4��
b������b����4��
��������ʽΪ��y��x2��4x+c��OB��OC�����B����Ϊ����c��0����
�ѵ�B������뺯������ʽ����ã�c����5��
��b����4��c����5��
��2�����κ�������ʽΪ��y��x2+4x��5��
�����Գ���Ϊx��2�����E����Ϊ��2����9����
�ѵ�E��B�������һ�κ�������ʽ��
y��mx+n�ã�![]() ����ã�
����ã�![]() ��
��
��ֱ��BE�ı���ʽΪ��y��3x��15��
������ã���F���ĺ�����Ϊ4����x��4������ʽ�ã�y��3��4��15����3
����������ΪF�䣨4����3����
����F��������0����3��
��3���裺Q��ֱ��PN�ľ���Ϊd����P����Ϊ��m��0�������N��m��m2��4m��5����
ֱ��B��C�ı���ʽΪ��y��x��5��
���M��m��m��5����
S��APM��![]() ��PM��AP��
��PM��AP��![]() ��0��m+5����m+1������
��0��m+5����m+1������![]() ��m2��4m��5����
��m2��4m��5����
S��PQN��![]() ��PN��d����
��PN��d����![]() ��m2��4m��5��d��
��m2��4m��5��d��
��S��PQN��S��APM��
��d��1��
��Q��ֱ��PN�ľ���Ϊ1��


 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д� �����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
�����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д� �����ҵ�����������ѧ���ӳ�����ϵ�д�
�����ҵ�����������ѧ���ӳ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��Բ��ֽƬ��С����������������������
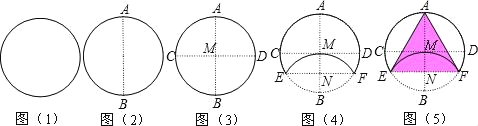
��1����Բ��ֽƬ���Ҷ��ۣ��ۺ�ΪAB����ͼ��2����ʾ��
��2����Բ��ֽƬ�����۵���ʹA��B�����غϣ��ۺ�CD��AB�ཻ��M����ͼ��3����ʾ��
��3����Բ��ֽƬ��EF�۵���ʹB��M�����غϣ��ۺ�EF��AB�ཻ��N����ͼ��4����ʾ��
��4������AE��AF����ͼ��5����ʾ��
�������ϲ���С���õ������½��ۣ�
��CD��EF�����ı���MEBF�����Σ��ۡ�AEFΪ�ȱ������Σ���![]() ��
��
���Ͻ�����ȷ���У�������
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���� O ����ABC �ı� AB ��һ�㣬�� OB Ϊ�뾶����O �� BC �ڵ� D������ D �����߽� AC �ڵ� E���� DE��AC��
(1)֤����AB��AC��
(2)�� AB��![]() cm��BC��2cm������ O �� AB ���ƶ���ʹ��O ��� AC ����ֱ������ʱ�� ����O �İ뾶��
cm��BC��2cm������ O �� AB ���ƶ���ʹ��O ��� AC ����ֱ������ʱ�� ����O �İ뾶��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ��� y=kx+b�뷴�������� y=![]() ��x��0����ͼ������A��m��6��B��3��n��������
��x��0����ͼ������A��m��6��B��3��n��������
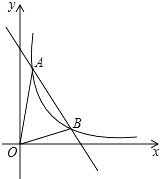
��1����һ�κ����Ľ���ʽ��
��2������AOB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵꾭��һ��˫�������֪����˫����ijɱ���Ϊÿ��30Ԫ���г����鷢�֣�����˫���ÿ���������y����λ:���������۵���x����λ:Ԫ�������¹�ϵ��y=��x+60��30��x��60����
������˫���ÿ�����������ΪwԪ��
��1����w��x֮��ĺ�������ʽ��
��2������˫������۵��۶�Ϊ����Ԫʱ��ÿ����������������������Ƕ���Ԫ��
��3�������۲��Ź涨����˫��������۵��۲�����48Ԫ�����̵���������˫���ÿ��Ҫ���200Ԫ�������������۵���Ӧ��Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���α�����һ����ҵ�⣺
��һ������������ABC�����ı�BC=120mm����AD=80mm��Ҫ�����ӹ��������������ʹ�����ε�һ����BC�ϣ�������������ֱ���AB��AC�ϣ��ʼӹ��ɵ�����������ı߳��Ƕ���mm��
Сӱ��ô���Ĵ�Ϊ48mm��Сӱ���ڷ�˼��������������µ����⣮
��1�����ԭ����Ҫ�ӹ��������һ�����Σ��Ҵ˾��������������ŷ��õ�����������ɣ���ͼ1����ʱ�������������������߳��ֱַ�Ϊ����mm��������㣮
��2�����ԭ������Ҫ�ӹ������ֻ��һ�����Σ���ͼ2���������˾�������������߳��Ͳ���ȷ���������������������ֵ����ﵽ������ֵʱ��������������߳���
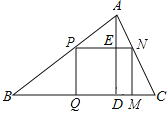
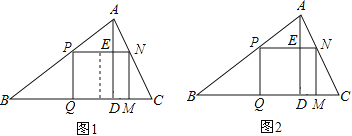
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2+2x+m��2=0������ʵ������mΪ���������Ҹ÷��̵ĸ��������������������������������m�ĺ�Ϊ��������
A. 6 B. 5 C. 4 D. 3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
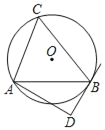
����Ŀ����ͼ����O�İ뾶Ϊ5����ABC�ǡ�O���ڽ������Σ�AB��8��AD����B�������ഹֱ������ΪD��
��1����֤����BAD+��C��90�㣻
��2�����߶�AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С��ͬѧ�����Ƶ�ֱ��������ֽ��DEF������AB�ĸ߶ȣ��������Լ���λ�ã��跨ʹб��DF����ˮƽ�����ұ�DE���B��ͬһֱ���ϣ���ֽ֪�������ֱ�DZ�DE��40cm��EF��20cm����ñ�DF�����ĸ߶�AC��1.5m��CD��8m������AB�ĸ߶ȣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com